Исследование кривых свободной поверхности потока в открытых призматических руслах

Неравномерное движение воды с нулевым и обратным уклоном.

Равномерное движение может устанавливаться только в русле с прямым уклоном дна, поэтому в руслах с нулевым и обратным уклоном нормальной глубины не существует. Таким образом, формулу (*) мы не сможем применять.

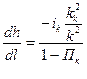для нулевого уклона,

где i_k; k_k – критический уклон и расходная характеристика при критическом уклоне.

для обратного

При неравномерном движении кривые свободной поверхности приближаются к линиям нормальной или критической глубины при уклоне большем нуля, которые остаются постоянными на протяжении всей длины.

1) глубина неравномерного движения стремится к нормальной

h → h₀ следовательно k → k₀; → 0, тогда

О

h₀

O

Если производная стремится к нулю, то это означает, что глубина стремится стать постоянной по длине потока, а кривая свободной поверхности асимптотически приближается к линии нормальной глубины.

2) h → h_kр. Следовательно (*) знаменатель стремится к нулю и

→ ∞.

К

К

h_i

Если глубина приближается к критической, то производная стремится к бесконечности и следовательно функция h в этой точке претерпевает разрыв. Кривая свободной поверхности теоретически должна проходить нормально к линии критической глубины, но опыт показывает, что кривая свободной поверхности подходит к линии критической глубины под крутым углом, но не прямы.

3) h → ∞, тогда k → ∞, ω → ∞, следовательно → i

В этом случае поверхность стремиться стать горизонтальной. Обычно это наблюдается в водопроводах и водоемах с большой глубиной.

Исследование форм свободной поверхности при i<i_k.

h₀ I

II

h_k

III

i < i_k

I зона.

h>h₀, h>h_k, > 0

l

П_к>1 П_к<1

h_k,П_к=1 h

Это означает, что глубина вдоль движения возрастает. Она может изменяться от нормальной глубины до весьма большой. В начале кривая асимптотически приближается к линии нормальной глубины, а затем стремится стать горизонтальной.

Кривая подпора

К

I_a

К

II зона.

h<h₀, h>h_k,

II_a

O O

K K

Кривая спада

III зона.

h<h₀<h_k, > 0

K

K

Кривая подпора III_a

Всего существует 12 типов кривых. Для построения кривой свободной поверхности предварительно необходимо установить форму кривой и исходные сечения. Такими сечениями могут быть сечения, где глубины известны, сечения перед перепадом при изменении уклона и т.д. После установления формы и исходного сечения необходимо определить количественные характеристики этой кривой.h=h(l), то есть проинтегрировать . Точных методов интегрирования нет.

1. Метод Чарновского.

Основан на непосредственном решении уравнения, в которое глубина входит в неявном виде.

2. Способ Павловского.

Основан на интегрировании дифференциального уравнения для призматических русел (i>0, i<0, i=0).

Дата добавления: 2014-01-04