Применение степенных рядов. Пример 7. Вычислить sin1 с точностью =0,01

Пример 7. Вычислить sin1 с точностью 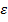=0,01.

Решение. Имеем .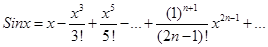

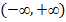
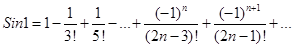
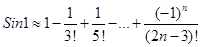,при этом ошибка будет равна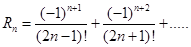

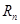называется остатком ряда. 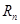является знакочередующимся рядом, который удовлетворяет всем условиям теоремы Лейбница. Следовательно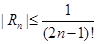. Если 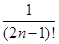<0.01, то 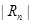<0,01. Подберем наименьшее n, для которого 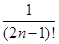<0.01, n=2 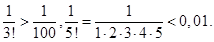Следовательно, 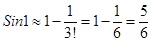, причем ошибка будет меньше 0,01.

Пример 8. Вычислить 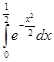с точностью 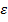=0,01.

Решение. Неопределенный интеграл 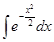не выражается в элементарных функциях, поэтому формулу Ньютона-Лейбница при вычислении данного интеграла применять нельзя.

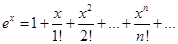
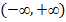
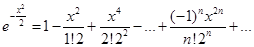
Последнее равенство проинтегрируем почленно на отрезке [0,].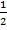

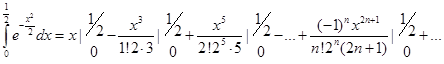
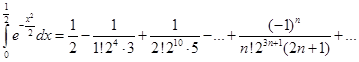
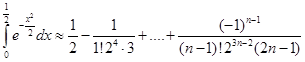. Ошибка будет равна .

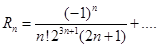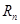является знакочередующимся рядом, который удовлетворяет всем условиям теоремы Лейбница. Следовательно 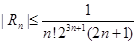. Если 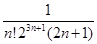<0,01, то и 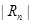<0,01. Для этого достаточно положить n=2. В самом деле, 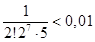. . 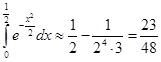При этом ошибка будет меньше 0,01.

Дата добавления: 2014-01-04