Закраска методом Гуро

Один из способов устранения дискретности интенсивностей закрашивания был предложен Гуро. Его метод заключается в том, что используются не нормали к плоским граням, а нормали к аппроксимируемой поверхности, построенные в вершинах многогранника. После этого вычисляются интенсивности в вершинах, а затем во всех внутренних точках многоугольника выполняется билинейная интерполяция интенсивности.

Метод сочетается с алгоритмом построчного сканирования. После того как грань отображена на плоскость изображения, для каждой сканирующей строки определяются ее точки пересечения с ребрами. В этих точках интенсивность вычисляется с помощью линейной интерполяции интенсивностей в вершинах ребра. Затем для всех внутренних точек многоугольника, лежащих на сканирующей строке, также вычисляется интенсивность методом линейной интерполяции двух полученных значений. На рис. 9.5 показан плоский многоугольник с вычисленными значениями интенсивностей в вершинах.

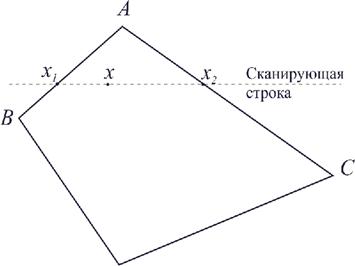
Рис. 9.5. Интерполяция интенсивности

Пусть - интенсивности в вершинах , 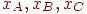- горизонтальные координаты этих точек. Тогда в точках пересечения сканирующей строки с ребрами многоугольника интенсивности можно вычислить по формулам интерполяции:

(9.7)

После этого интенсивность в точке 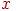получаем путем интерполяции значений на концах отрезка:

(9.8)

К недостаткам метода Гуро следует отнести то, что он хорошо работает только с диффузной моделью отражения. Форма бликов на поверхности и их расположение не могут быть адекватно воспроизведены при интерполяции на многоугольниках. Кроме того, есть проблема построения нормалей к поверхности. В алгоритме Гуро нормаль в вершине многогранника вычисляется путем усреднения нормалей к граням, примыкающим к этой вершине. Такое построение сильно зависит от характера разбиения.

Дата добавления: 2014-01-04