Лекция №4. Тема 1.3 Методы решения краевых задач

Тема 1.3 Методы решения краевых задач. Метод разделения переменных (Метод Фурье).

Метод разделения переменных относится к классическим методам решения линейного дифференциального уравнения теплопроводности. При его применении вначале находится совокупность частных решений линейного однородного дифференциального уравнения теплопроводности, удовлетворяющих однородным граничным условиям, затем в силу принципа суперпозиций составляется ряд из этих решений.

где коэффициенты 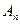определяются из начальных условий.

Метод применим для конечных областей.

Рассмотрим метод Фурье применительно к следующей задаче

(23)

().

В случае декартовых координат ;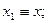

;

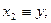
- конечная пространственная область.

Предположим, что ГУ приведены к однородным. Тогда, частное решение уравнения (23) ищем в виде произведения двух функций

, (24)

одна из которых зависит только от времени, а другая - только от пространственных координат; А- произвольная постоянная.

Если (24) подставить в (23), то получим два дифференциальных уравнения относительно

; (25)

относительно

; (26)

где - постоянная разделения.

Решение (25) элементарно

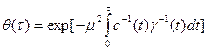
Решение (26) получено лишь для некоторых частных случаев.

Задача нахождения тех значений постоянной , для которых существуют нетривиальные решения уравнения (26) (называется собственными функциями), удовлетворяющие граничным условиям, называется задачей Штурма-Лиувилля.

При постоянном коэффициенте 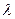задача Штурма-Лиувилля решена для тел, образованных пересечением координатных поверхностей в различных системах координат. Например, для одномерной задачи решение уравнения (26) имеет вид

в прямоугольных координатах

; (27)

в сферических координатах

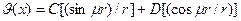; (28)

в цилиндрических координатах

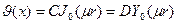, (29)

где С, D – произвольные постоянные; а числа 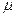определяются из граничных условий задачи; 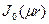- функция Бесселя первого ряда нулевого порядка; - функция Бесселя второго рода нулевого порядка.

Определив выражения для функций и 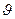, решение уравнения (23) с соответствующими ГУ представится в виде

,

где - собственные функции, отвечающие собственным числам .

Определим коэффициенты 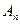из начального условия [при ]

,

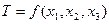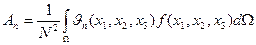где - рассматриваемая конечная область; N – норма собственной функции , равная

.

При этом используется ортогональность собственных функций 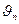, является свойством собственных функций задачи Штурма-Лиувилля.

Окончательно решение краевой задачи имеет вид

. (30)

При условии, что ряд (30) допускает почленное дифференцирование дважды по пространственным координатам и один раз по времени.

Нагрев неограниченной пластины.

Дана неограниченная пластина, толщина которой равна 2R. В начальный момент времени пластина помещается в среду с постоянной температурой 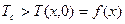. Между ограничивающими поверхностями пластины и окружающей средой происходит теплообмен по закону Ньютона. Найти распределение температуры по толщине пластины в любой момент времени.

Дифференциальное уравнение теплопроводности и его краевые условия имеют вид

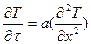, , -R<x<R, (31)

T(x,0)=f(x); (32)

; (33)

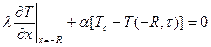. (34)

Решение проведем методом разделения переменных. Предположим, что функция 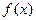четная, то есть , поэтому . Тогда вместо граничного условия (34) можно записать

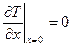. (35)

Введем новую функцию , позволяющую свести задачу на нагревание к задаче на охлаждение. Очевидно, что исходное дифференциальное уравнение относительно функции не изменится, а граничное условие (33) приведется к однородному виду. Частное решение задачи будем искать в виде

.

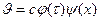После подстановки в уравнение (31) получим

.

Интегрирование уравнения дает .

Дифференциальное уравнение для определения имеет вид

.

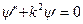Известно общее решение этого уравнения

.

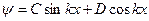Тогда частное решение уравнения (31) примет следующий вид

.

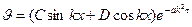Из условия симметрии процесса теплопроводности (35) следует

.

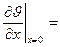
Это означает, что 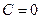, тогда

.

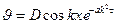Значение постоянной разделения определим, удовлетворяя ГУ (32). Имеем

;

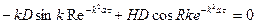, (36)

где 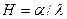- относительный коэффициент теплоотдачи.

Преобразовав уравнение (36), получим

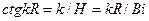, (37)

где .

Обозначив через 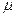, характеристическое уравнение (37) можно написать в виде

.

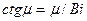Корни этого уравнения приведены в Т 2.1 [1].

Следовательно, общее решение краевой задачи (31)-(35) имеет вид

.

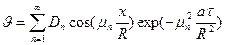Для определения постоянных воспользуемся начальным условием (32) и ортогональностью функций 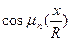в промежутке [-R; R]

.

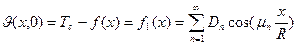Умножим обе части этого равенства на и проинтегрируем в промежутке [-R; R], тогда получим соотношение для коэффициентов

. (38)

Общее решение задачи с учетом соотношения (38)

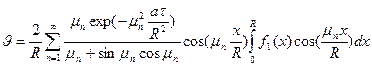. (39)

Для случая, когда 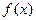является нечетной функцией, частное и общее решения задачи соответственно имеют следующий вид

;

,

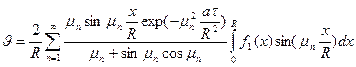где - корни трансцендентного уравнения .

Первые шесть корней этого уравнения приведены в Т 2.2[1] для различных значений Bi.

При равномерном начальном распределении температуры, то есть f(x)=, распределение температуры (39) в безразмерной форме

.

Дата добавления: 2014-01-04