Тема 1.7 Нагрев цилиндра конечных размеров

Лекция №8

. (105)

Если имеется симметрия относительно оси z, то оператор тождественно равен нулю, тогда получим

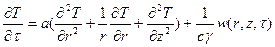. (106)

1). Рассмотрим решение уравнения для конечного цилиндра длиной l при ГУ2 на боковой поверхности.

Положим, что один из торцов (z=0) теплоизолирован.

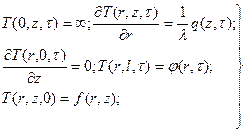(107)

Используем преобразования Ханкеля и Фурье для решения этой задачи.

Для простоты последующих выкладок запишем уравнение (105) и условия (106) в безразмерной форме

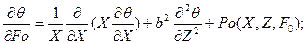(108)

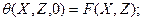(109)

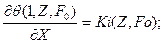(110)

(111)

где 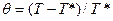- безразмерная температура (Т* - некоторое начальное значение температуры, фиксированная для определенной точки цилиндра); 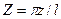- безразмерные координаты.

; ;

; ;

.

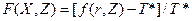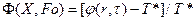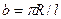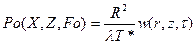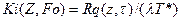Воспользуемся по переменной Х конечным интегральным преобразованием Ханкеля

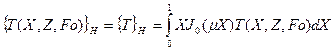(112)

и формулой обращения

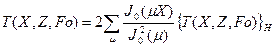, (113)

где 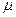- положительный корень характеристического уравнения ;

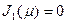а по переменной Z – конечным косинус-преобразованием Фурье

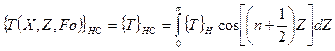(114)

и формулой обращения

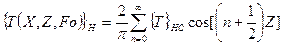(115)

Согласно приведенным преобразованиям получим решение задачи в следующем виде

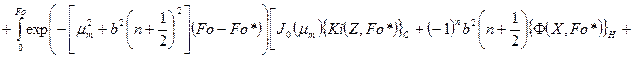
(116)

Если принять в (115) и 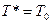, то найдем

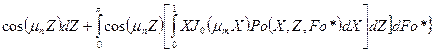, (117)

где 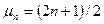(n=0, 1, 2,…)

2). Рассмотрим теперь решение уравнения (106) при выполнении ГУ3 на боковой поверхности цилиндра.

Пусть краевые условия задачи имеют вид

;

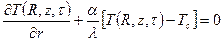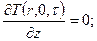
или в безразмерной форме

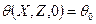; (118)

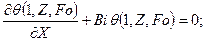(119)

(120)

В уравнении (108) и условиях (118)-(120) в отличие от предыдущей задачи безразмерный потенциал имеет вид

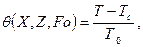
кроме того

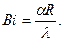
Применяя к уравнению (107) и условиям (117)-(119) последовательно преобразования (111) и (113), найдем обыкновенное неоднородное дифференциальное уравнение в изображениях. Решая его и выполняя обратные интегральные преобразования (115) и (113), после некоторых упрощений получим окончательное решение

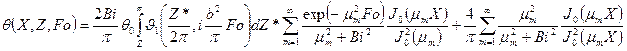
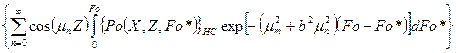(121)

где ,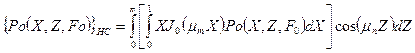

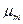- положительные корни характеристического уравнения

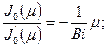
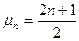, (n=0, 1, 2,…).

В (121) введено разложение для тета-функции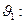

Дата добавления: 2014-01-04