
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 9.§144. Центр линии второго порядка
|
|
|
|
Аналитическая геометрия.
Глава 11. Линии второго порядка, заданные общими уравнениями
Определение. Центром линии второго порядка называется центр симметрии этой линии, т.е. точка 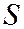 , обладающая следующим свойством: если на линии лежит точка (действительная или мнимая)
, обладающая следующим свойством: если на линии лежит точка (действительная или мнимая) 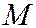 , то на этой же линии лежит точка
, то на этой же линии лежит точка 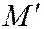 , симметричная точке
, симметричная точке 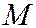 относительно
относительно 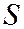 .
.
Теорема 1. Пусть относительно ОДСК задана линия второго порядка общим уравнением:
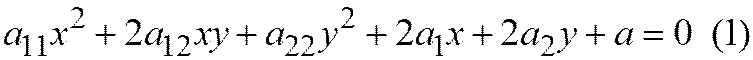
Для того, чтобы начало координат являлось её центром, необходимо и достаточно, чтобы в уравне-нии (1) отсутствовали члены с 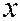 и
и 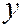 в первой степени, т.е., чтобы
в первой степени, т.е., чтобы  . Иначе, чтобы уравнение линии имело вид:
. Иначе, чтобы уравнение линии имело вид:  . (2)
. (2)
Доказательство достаточности. Если  , то уравнение линии имеет вид (2), и, если ему удовлет-воряют координаты
, то уравнение линии имеет вид (2), и, если ему удовлет-воряют координаты 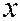 и
и 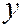 точки
точки 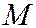 , то ему удовлетво-ряют и координаты
, то ему удовлетво-ряют и координаты 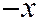 и
и 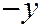 точки
точки 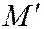 , симметричной
, симметричной 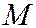 относительно начала координат.
относительно начала координат.
Доказательство необходимости. Пусть начало ко-ординат является центром линии (1). Предположим вопреки утверждению теоремы, что по крайней мере одно из чисел 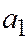 или
или 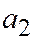 отлично от нуля. Возьмём на линии (1) произвольную точку
отлично от нуля. Возьмём на линии (1) произвольную точку 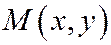 . Её координа-ты удовлетворяют уравнению (1), а так как начало координат является центром симметрии линии (1), то уравнению (1) удовлетворяют и координаты точки
. Её координа-ты удовлетворяют уравнению (1), а так как начало координат является центром симметрии линии (1), то уравнению (1) удовлетворяют и координаты точки 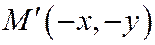 симметричной точке
симметричной точке 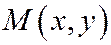 относитель-но начала координат, то есть
относитель-но начала координат, то есть
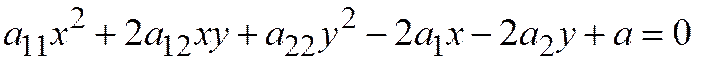
Из этого соотношения и из соотношения (1) находим:
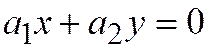 , то есть
, то есть 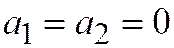 . ЧТД.
. ЧТД.
Теорема 2. Если относительно ОДСК линия второ-го порядка задана общим уравнением (1), то координаты 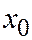 ,
,  её центра определяются из системы уравнений:
её центра определяются из системы уравнений:  (2)
(2)
причём в случае несовместности этой системы, линия не имеет центра (т.е. является параболой).
Доказательство. Произведём перенос Декартовой системы так, чтобы новым началом координат стала точка 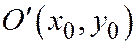 . Обозначая координаты про-извольной точки
. Обозначая координаты про-извольной точки 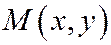 в новой системе
в новой системе 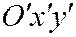 через
через 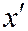 ,
,  , будем иметь:
, будем иметь: 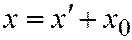 ;
; 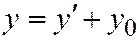 , и уравнение (1) примет вид
, и уравнение (1) примет вид
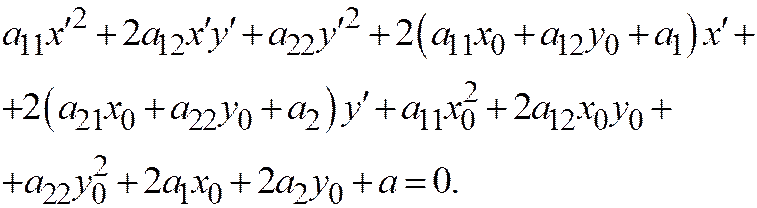 На основании предыдущей теоремы 1 точка
На основании предыдущей теоремы 1 точка 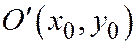 является центром данной линии тогда и только тогда, когда, когда:
является центром данной линии тогда и только тогда, когда, когда: 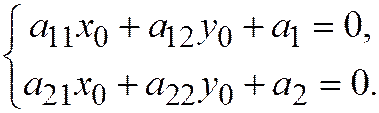
Теперь, если 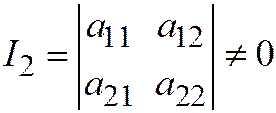 , то система (2) имеет единственное решение, т.е. линия (1) имеет единственный центр. Если система (2) несовместна, то линия не имеет центра, т.е. является параболой. Если система (2) неопределённая, т.е. имеет бесчисленное множество решений, то линия (1) имеет бесконечное множество центров - прямую центров, так как в случае неопределённости системы множество всех её реше-ний есть множество всех решений уравнения первой степени относительно
, то система (2) имеет единственное решение, т.е. линия (1) имеет единственный центр. Если система (2) несовместна, то линия не имеет центра, т.е. является параболой. Если система (2) неопределённая, т.е. имеет бесчисленное множество решений, то линия (1) имеет бесконечное множество центров - прямую центров, так как в случае неопределённости системы множество всех её реше-ний есть множество всех решений уравнения первой степени относительно 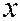 и
и 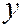 .
.
Данная ранее классификация линий второго порядка по группам I, II, III, является классификацией этих линий по характеру их места центров: линии группы I имеют единственный центр (начало координат в их простейшем уравнении); линии группы II не имеют центра (парабола); линии группы III имеют прямую центров (ось 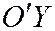 в простейшем уравнении). В этом можно убедиться, составляя систему уравнений (3) для определения центра для каждого из уравнений:
в простейшем уравнении). В этом можно убедиться, составляя систему уравнений (3) для определения центра для каждого из уравнений:
I. 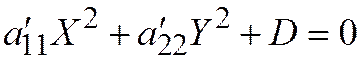 ,
,  ,
, 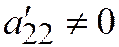 . Здесь
. Здесь 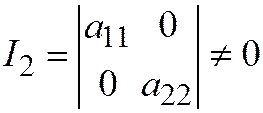 , система (3) равна
, система (3) равна  то есть центром является начало координат
то есть центром является начало координат  .
.
II. 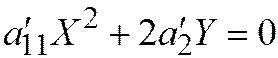 ,
,  ,
, 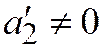 . Здесь
. Здесь 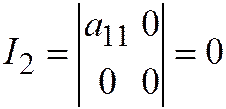 , система (3) равна
, система (3) равна 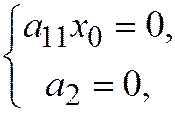 то есть решения нет и, значит, линия не имеет центра.
то есть решения нет и, значит, линия не имеет центра.
III. 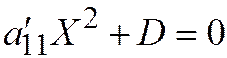 ,
,  . Здесь
. Здесь 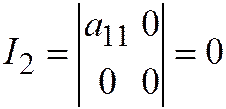 , система (3) равна
, система (3) равна 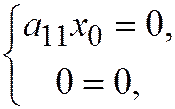 то есть
то есть 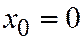 , а это ось
, а это ось 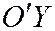 , значит, здесь целая прямая центров.
, значит, здесь целая прямая центров.
§ 145. Пересечение линии второго порядка с прямой. Асимптотические направления. Классификация линий второго порядка по числу и действительности асимптотических направлений.
Предположим, что относительно ОДСК задана линия второго порядка общим уравнением 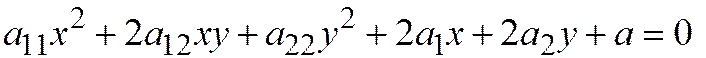 .
.
Будем искать пересечение этой линии с прямой, уравнения которой возьмём в параметрической форме: 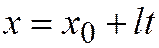 ,
, 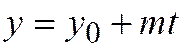 . Здесь
. Здесь 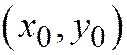 - некоторая точка прямой, а
- некоторая точка прямой, а 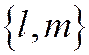 - её направляющий вектор. Для нахождения координат точек пересечения прямой
- её направляющий вектор. Для нахождения координат точек пересечения прямой 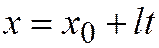 ,
, 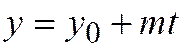 с линией (1) надо найти значения параметра
с линией (1) надо найти значения параметра  , при которых точка прямой лежит на линии (1). Подставляя в уравнение (1)
, при которых точка прямой лежит на линии (1). Подставляя в уравнение (1) 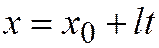 и
и 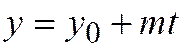 , получим:
, получим:
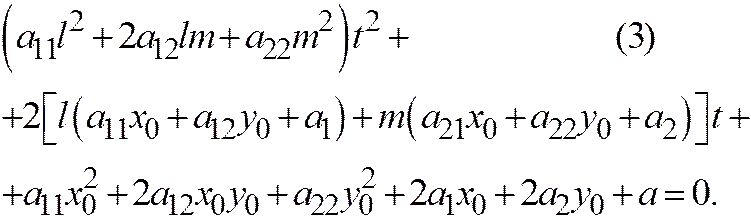
Если в этом уравнении коэффициент при 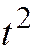 отличен от нуля, то уравнение (3) имеет два корня (действительных различных, мнимых различных, или действительных совпадающих), и, значит, прямая линия пересекает линию (1) в двух точках (соответственно действительных различных, комплексных сопряжённых, или действительных совпадающих).
отличен от нуля, то уравнение (3) имеет два корня (действительных различных, мнимых различных, или действительных совпадающих), и, значит, прямая линия пересекает линию (1) в двух точках (соответственно действительных различных, комплексных сопряжённых, или действительных совпадающих).
Если же 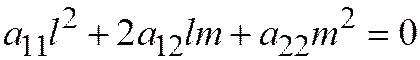 , (4)
, (4)
то прямая с направляющим вектором  либо пере-секает линию второго порядка только в одной точке (это будет тогда и только тогда, когда коэффициент при
либо пере-секает линию второго порядка только в одной точке (это будет тогда и только тогда, когда коэффициент при 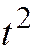 в уравнении (3) равен нулю, а коэффициент при
в уравнении (3) равен нулю, а коэффициент при  не равен нулю); либо не пересекает её (это бу-дет тогда и только тогда, когда коэффициенты при
не равен нулю); либо не пересекает её (это бу-дет тогда и только тогда, когда коэффициенты при 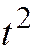 и
и  в уравнении (3) равны нулю, а свободный член не равен нулю); либо входит в состав данной линии (это будет тогда и только тогда, когда соотношение (3) яв-ляется тождеством относительно
в уравнении (3) равны нулю, а свободный член не равен нулю); либо входит в состав данной линии (это будет тогда и только тогда, когда соотношение (3) яв-ляется тождеством относительно  ).
).
Определение. Говорят, что прямая имеет асимптотическое направление по отношению к данной линии второго порядка, если координаты  её направляющего вектора удовлетворяют уравнению
её направляющего вектора удовлетворяют уравнению 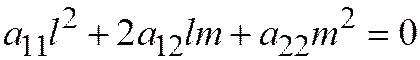 . Говорят также, что вектор
. Говорят также, что вектор  имеет асимптотическое направление.
имеет асимптотическое направление.
По отношению к асимптотическим направлениям линии второго порядка делятся на три типа:
А. Линии эллиптического типа: это линии второго порядка, не имеющие асимптотических направлений (эллипс, мнимый эллипс, две мнимые пересекающиеся прямые).
В. Линии гиперболического типа, имеющие два асимптотических направления (гипербола, две пересекающиеся прямые).
С. Линии параболического типа; это линии, имеющие одно асимптотическое направление (парабола, две параллельные или совпадающие прямые).
Теорема 3. Необходимым и достаточным условием того, что линия второго порядка, заданная общим уравнением (1) относительно ОДСК не имеет асимптотических направлений (действительных), т.е. явля-ется линией эллиптического типа, является условие:
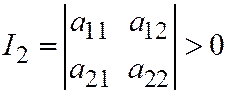 .
.
Необходимым и достаточным условием того, что линия второго порядка, заданная общим уравнением (1) относительно ОДСК имеет два различных действительных асимптотических направления т.е. является линией гиперболического типа, является условие:
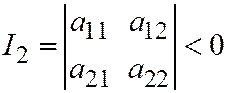 .
.
Необходимым и достаточным условием того, что линия второго порядка, заданная общим уравнением (1) относительно ОДСК имеет только одно асимптотическое направление т.е. является линией параболического типа, является условие:
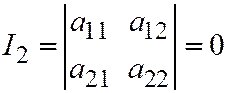 .
.
Доказательство. Координаты вектора  , имеющего асимптотическое направление, определяются из уравнения
, имеющего асимптотическое направление, определяются из уравнения 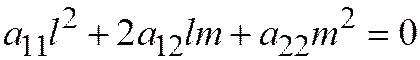 .
.
Так как вектор  ненулевой, то имеет смысл рассматривать по крайней мере одно из соотношений:
ненулевой, то имеет смысл рассматривать по крайней мере одно из соотношений: 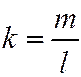 ; или
; или  . Уравнение
. Уравнение 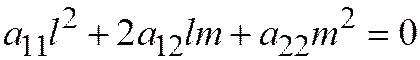 , следовательно, эквива-лентно одному из уравнений (или
, следовательно, эквива-лентно одному из уравнений (или 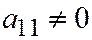 , или
, или 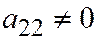 ):
):
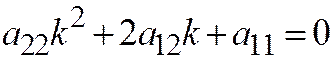 ; или
; или 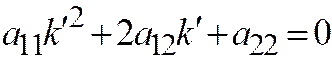 .
.
Для того, чтобы решения любого из этих уравнений были комплексными (сопряжёнными), Действительными различными, или совпадающими, необходимо и достаточно, чтобы выполнялось, соответственно, условие 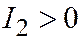 ;
; 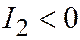 ;
;  .
.
В первом случае (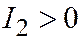 , при этом дискриминант квадратного уравнения
, при этом дискриминант квадратного уравнения 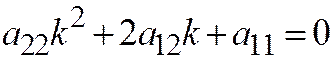 :
: 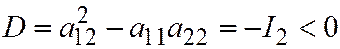 ), линия не имеет действительных асимптотических направлений и является линией эллиптического типа; во втором случае (
), линия не имеет действительных асимптотических направлений и является линией эллиптического типа; во втором случае (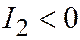 ,
, 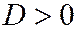 ), линия имеет два различных асимптотических направления и является линией гиперболического типа; в третьем случае (
), линия имеет два различных асимптотических направления и является линией гиперболического типа; в третьем случае ( ,
, 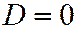 ), линия имеет одно (действительное) асимптотическое направление и является линией параболического типа. В последнем третьем случае угловой коэффициент
), линия имеет одно (действительное) асимптотическое направление и является линией параболического типа. В последнем третьем случае угловой коэффициент 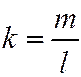 единственного асимптотического направления определяется одним из соотношений:
единственного асимптотического направления определяется одним из соотношений:  или
или 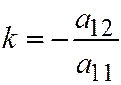 .
.
Если 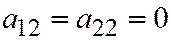 , то асимптотическим направлением является направление оси
, то асимптотическим направлением является направление оси 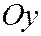 , т.к. уравнение, определяющее координаты векторов, имеющих асимптотические направления
, т.к. уравнение, определяющее координаты векторов, имеющих асимптотические направления 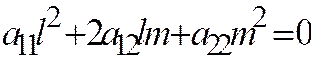 , принимают вид:
, принимают вид:  , откуда
, откуда 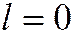 . (Ну, напри-мер, возьмём параболу
. (Ну, напри-мер, возьмём параболу 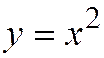 , перепишем это урав-нение в виде
, перепишем это урав-нение в виде 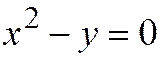 . Здесь
. Здесь 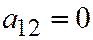 ,
, 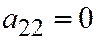 . Но ведь мы с Вами хорошо знаем, что у параболы
. Но ведь мы с Вами хорошо знаем, что у параболы 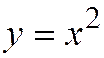 асимптотическим направлением является направление оси
асимптотическим направлением является направление оси 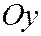 .
.
Остаётся рассмотреть случай 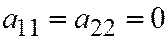 . Уравне-ние линии принимает вид:
. Уравне-ние линии принимает вид: 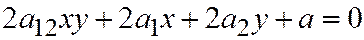 , а уравнение, из которого находятся координаты векторов, имеющих асимптотические направления:
, а уравнение, из которого находятся координаты векторов, имеющих асимптотические направления: 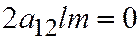 , следовательно, либо
, следовательно, либо 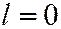 , либо
, либо 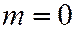 , т.е. линия имеет два различных асимптотических направления - направления осей координат. (Заметим, что
, т.е. линия имеет два различных асимптотических направления - направления осей координат. (Заметим, что 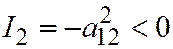 , значит, линия гиперболического типа.
, значит, линия гиперболического типа.
Обратно, если оси координат имеют асимптотичес-кие направления, то уравнение 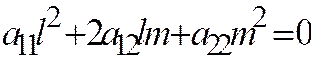
должно удовлетворяться и при 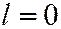 , и при
, и при 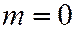 , т.е.
, т.е. 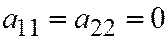 . Значит, уравнение линии имеет вид:
. Значит, уравнение линии имеет вид: 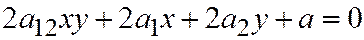 .
.
Рассмотрим примеры. Для гиперболы 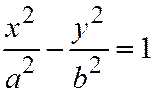 или для двух пересекающихся прямых
или для двух пересекающихся прямых  координаты
координаты  векторов, имеющих асимптотические направления, определяются из уравнения
векторов, имеющих асимптотические направления, определяются из уравнения 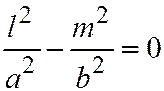 , т.е. это, соответственно, или направления асимптот гиперболы, или (если это две пересекающиеся прямые) направления рассматриваемых прямых.
, т.е. это, соответственно, или направления асимптот гиперболы, или (если это две пересекающиеся прямые) направления рассматриваемых прямых.
Для параболы 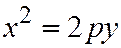 уравнение, определяющее координаты вектора
уравнение, определяющее координаты вектора  асимптотического направления, имеют вид:
асимптотического направления, имеют вид: 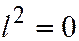 , т.е.
, т.е. 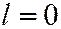 , значит, асимптотическое направление параболы есть направление её оси.
, значит, асимптотическое направление параболы есть направление её оси.
Если, наконец, уравнение линии второго порядка определяет две параллельные (или совпадающие) прямые, то асимптотическим направлением является направление этих прямых.
Глава 11. Линии второго порядка, заданные общими уравнениями
§ 146. Диаметр, сопряжённый данному неасимптотическому направлению
I. Общая теория.
Теорема 1. Геометрическим местом середин хорд линии второго порядка, параллельных вектору неасимптотического направления, является прямая линия; эта прямая линия называется диаметром данной линии, сопряжённым рассматриваемым параллельным хордам. Если линия второго порядка задана относительно ОДСК общим уравнением 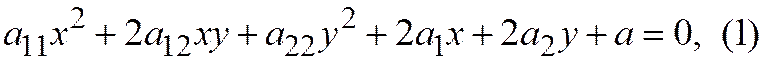 а её хорды параллельны ненулевому вектору
а её хорды параллельны ненулевому вектору  (неасимптотического направления), то уравнение диаметра, сопряжённого этим хордам имеет вид:
(неасимптотического направления), то уравнение диаметра, сопряжённого этим хордам имеет вид:
 . (2)
. (2)
Доказательство. Пусть прямая 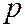 , коллинеарная вектору
, коллинеарная вектору  неасимптотического направления по отношению к линии (1), пересекает эту линию в точках
неасимптотического направления по отношению к линии (1), пересекает эту линию в точках 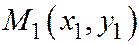 и
и 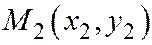 . Обозначим через
. Обозначим через 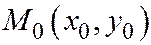 середину отрезка
середину отрезка 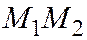 . Уравнение ука-занной прямой можно записать в виде
. Уравнение ука-занной прямой можно записать в виде 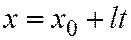 ,
, 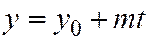 . Значения параметра
. Значения параметра 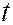 , соответствующие координатам точек
, соответствующие координатам точек 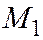 и
и 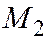 , определяются из уравнения
, определяются из уравнения
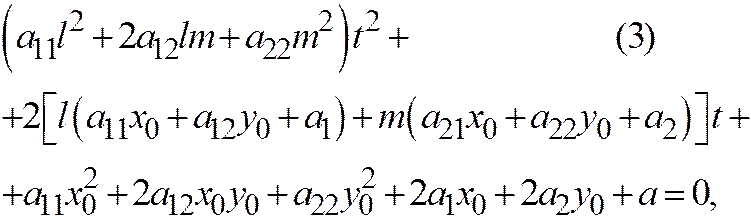
которое получим, подставив в уравнение (1) вместо 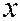 и
и 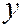 их выражения из формул
их выражения из формул 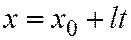 ,
, 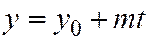 .
.
Пусть 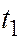 и
и 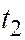 - корни этого уравнения. Так как
- корни этого уравнения. Так как 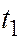 и
и
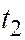 - это координаты точек
- это координаты точек 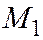 и
и 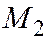 на прямой
на прямой 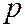 с началом координат в точке
с началом координат в точке 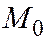 и масштабным векто-ром
и масштабным векто-ром 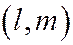 , а точка
, а точка 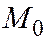 - середина отрезка
- середина отрезка 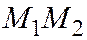 , то точка
, то точка 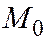 на прямой
на прямой 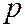 в указанной системе координат имеет координату
в указанной системе координат имеет координату  , а так как с другой стороны из соотношений
, а так как с другой стороны из соотношений 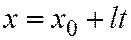 ,
, 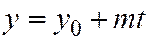 ясно, что
ясно, что 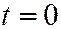 для точки
для точки 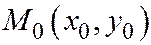 , то
, то 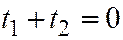 и (т.к. по теореме Виета
и (т.к. по теореме Виета 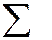 корней) поэтому
корней) поэтому 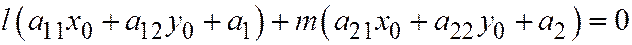 .
.
Это соотношение, таким образом, является необ-ходимым и достаточным условием того, что хорда, имеющая направление вектора  точкой
точкой 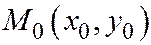 делится пополам. С другой стороны, каждая прямая, параллельная вектору
делится пополам. С другой стороны, каждая прямая, параллельная вектору  , пересекает линию (1) в двух точках (действительных различных, мнимых различных или действительных совпадающих); (для каждой прямой, параллельной вектору
, пересекает линию (1) в двух точках (действительных различных, мнимых различных или действительных совпадающих); (для каждой прямой, параллельной вектору  , координаты
, координаты 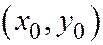 меняются, но всякий раз они удовлетворяют уравнению первой степени), поэтому геометрическим местом середин хорд линии (1), параллельных вектору
меняются, но всякий раз они удовлетворяют уравнению первой степени), поэтому геометрическим местом середин хорд линии (1), параллельных вектору  , является вся прямая, уравнение которой имеет вид:
, является вся прямая, уравнение которой имеет вид:
 . (4)
. (4)
В этом уравнении коэффициенты при 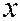 и
и 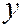 одно-временно в нуль не обращаются, так как, если бы мы имели
одно-временно в нуль не обращаются, так как, если бы мы имели 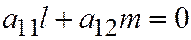 и
и  , то было бы выполнено и соотношение:
, то было бы выполнено и соотношение:
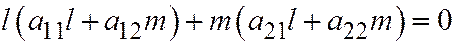 или
или
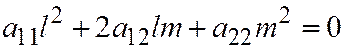 , т.е. вектор
, т.е. вектор  имел бы асимптотическое направление.
имел бы асимптотическое направление.
Из уравнения (4), рассматривая его как уравнение прямой в общем виде 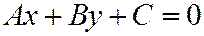 , находим координаты
, находим координаты  направляющего вектора диаметра, сопряжённого хордам, параллельным ненулевому вектору
направляющего вектора диаметра, сопряжённого хордам, параллельным ненулевому вектору  :
: 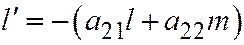 ,
, 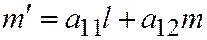 . (5)
. (5)
Умножая первое из этих соотношений на 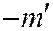 , а второе на
, а второе на 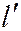 и складывая, получим:
и складывая, получим:
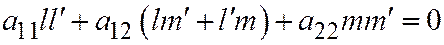 . (6)
. (6)
Таково необходимое и достаточное условие, связывающее координаты ненулевого вектора  , параллельного хордам линии второго порядка, заданной общим уравнением (1) относительно ОДСК, и координаты ненулевого вектора
, параллельного хордам линии второго порядка, заданной общим уравнением (1) относительно ОДСК, и координаты ненулевого вектора  , параллельного диаметру, сопряженному этим хордам.
, параллельного диаметру, сопряженному этим хордам.
(Вектор  ненулевой, т.к. в противном случае из соотношений
ненулевой, т.к. в противном случае из соотношений 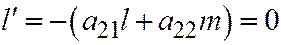 ,
, 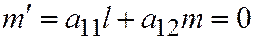 мы бы получили, что
мы бы получили, что
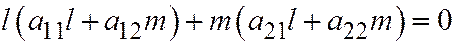 , или
, или
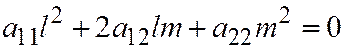 , т.е. вектор
, т.е. вектор  имел бы асимптотическое направление).
имел бы асимптотическое направление).
Соотношение (6) выполняется для асимптотического направления линии второго порядка, если в нём положить 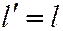 и
и 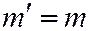 (так как тогда мы получим
(так как тогда мы получим 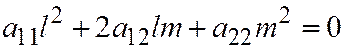 ), поэтому асимптотическое направление линии второго порядка часто называют самосопряжённым.
), поэтому асимптотическое направление линии второго порядка часто называют самосопряжённым.
Теорема 2. Если линия второго порядка является линией, имеющей единственный центр, и, если рассмотреть семейство параллельных хорд этой линии, не имеющей асимптотического направления, то диаметр, им сопряжённый, также не имеет асимптотического направления; если взять семейство хорд линии второго порядка, параллельных этому диаметру, то диаметр, им сопряжённый, будет параллелен хордам первоначального семейства.
Доказательство. Пусть относительно ОДСК задана линия второго порядка общим уравнением: 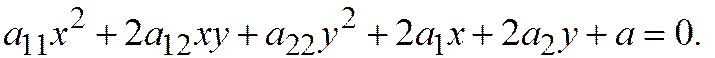 Предположим, что эта линия имеет единственный центр, т.е.
Предположим, что эта линия имеет единственный центр, т.е. 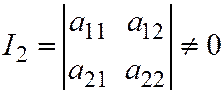 . Возьмём любой ненулевой вектор
. Возьмём любой ненулевой вектор  , не имеющий асимптотического направления, и рассмотрим уравнение диаметра
, не имеющий асимптотического направления, и рассмотрим уравнение диаметра
 ,
,
Сопряжённого хордам, параллельным вектору  . Направляющий вектор
. Направляющий вектор  этого диаметра имеет координаты:
этого диаметра имеет координаты: 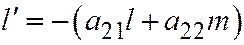 ,
, 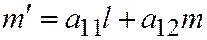 . Векторы
. Векторы  и
и  неколлинеарны, так как
неколлинеарны, так как 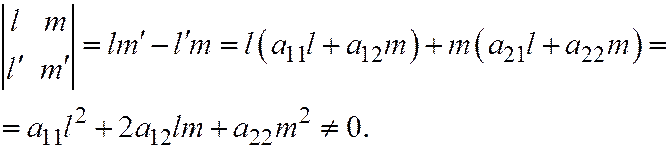
Вектор  не имеет асимптотического направления. В самом деле, так как
не имеет асимптотического направления. В самом деле, так как 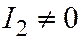 , то числа
, то числа 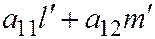 и
и 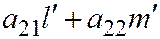 не обращаются в ноль одновременно. (Ну смотрите. Если определитель не равен нулю, то в каждом столбце должен быть хотя бы один ненулевой элемент, например:
не обращаются в ноль одновременно. (Ну смотрите. Если определитель не равен нулю, то в каждом столбце должен быть хотя бы один ненулевой элемент, например: 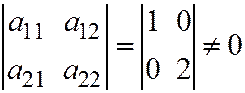 . Далее, вектор
. Далее, вектор  также ненулевой, то есть, или
также ненулевой, то есть, или 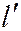 , или
, или 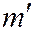 не равны нулю, например:
не равны нулю, например: 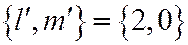 .
.
Тогда: 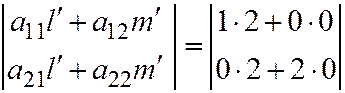 . Видно, что первый элемент ненулевой).
. Видно, что первый элемент ненулевой).
В связи с этим, уравнение: 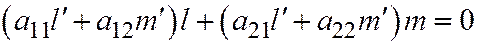 , (7) в котором
, (7) в котором  и
и 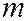 рассматриваются как неизвестные, не может иметь двух линейно независимых решений. Но одним из его решений является пара координат вектора
рассматриваются как неизвестные, не может иметь двух линейно независимых решений. Но одним из его решений является пара координат вектора  (т.к. это соотношение (6) в теореме 1), направлению которого сопряжен диаметр с направляющим вектором
(т.к. это соотношение (6) в теореме 1), направлению которого сопряжен диаметр с направляющим вектором  , неколлинеарным вектору
, неколлинеарным вектору  . Значит, координаты вектора
. Значит, координаты вектора  не удовлетворяют уравнению (7), то есть:
не удовлетворяют уравнению (7), то есть:
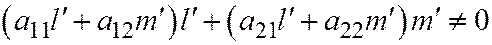 , или
, или
 , то есть
, то есть  - вектор, не имеющий асимптотического направления линии (1).
- вектор, не имеющий асимптотического направления линии (1).
Теперь, из соотношения (6):
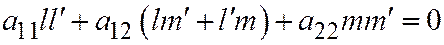 в силу его симметрии относительно пар чисел
в силу его симметрии относительно пар чисел  и
и 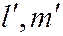 следует, что если линия второго порядка имеет единственный центр, то диаметр, сопряжённый хордам, параллельным вектору
следует, что если линия второго порядка имеет единственный центр, то диаметр, сопряжённый хордам, параллельным вектору  , коллинеарен вектору
, коллинеарен вектору  . Теорема доказана.
. Теорема доказана.
Определение. Два диаметра линии, имеющей единственный центр, из которых каждый делит пополам хорды, параллельные другому диаметру, называются сопряжёнными.
Условие 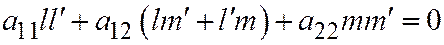 можно теперь интерпретировать как необходимое и достаточное условие сопряженности двух диаметров линии второго порядка, имеющей единственный центр и заданной общим уравнением (1) относительно ОДСК. Если
можно теперь интерпретировать как необходимое и достаточное условие сопряженности двух диаметров линии второго порядка, имеющей единственный центр и заданной общим уравнением (1) относительно ОДСК. Если  и
и 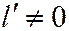 , то это необходимое и достаточное условие сопряженности можно записать в виде:
, то это необходимое и достаточное условие сопряженности можно записать в виде: 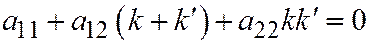 , где
, где 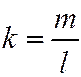 и
и 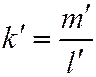 - угловые коэффициенты диаметров.
- угловые коэффициенты диаметров.
Теорема 3. Если линия второго порядка имеет единственный центр, то любая прямая неасимптотического направления, проходящая через её центр, является диаметром этой линии.
Доказательство. Если линия, заданная общим уравнением (1), имеет единственный центр, то прямые
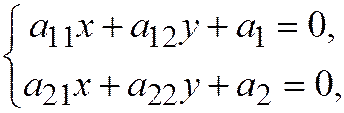 где
где 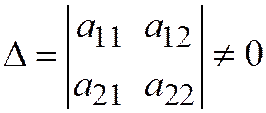 , пересекаются в её центре (поскольку Вы знаете, что это система для определения координат центра), но в таком случае уравнение любой прямой
, пересекаются в её центре (поскольку Вы знаете, что это система для определения координат центра), но в таком случае уравнение любой прямой 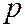 , проходящей через центр линии, можно записать в виде пучка прямых:
, проходящей через центр линии, можно записать в виде пучка прямых: 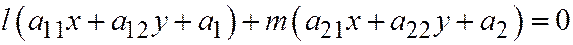 , где хотя бы одно из чисел
, где хотя бы одно из чисел  или
или 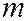 не равно нулю.
не равно нулю.
Значит, прямая 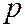 является диаметром линии, сопряжённым хордам, параллельным вектору
является диаметром линии, сопряжённым хордам, параллельным вектору  , если этот вектор неасимптотического направления. Но из неасимптотичности направления прямой
, если этот вектор неасимптотического направления. Но из неасимптотичности направления прямой 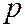 вытекает неасимптотичность сопряжённого ей направ-ления
вытекает неасимптотичность сопряжённого ей направ-ления  (теорема 2 настоящей лекции), следова-тельно прямая
(теорема 2 настоящей лекции), следова-тельно прямая 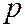 является диаметром. ЧТД.
является диаметром. ЧТД.
Теорема 4. Если линия второго порядка является линией параболического типа, то диаметр, сопряжён-ный хордам линии, параллельным неасимптотическо-му направлению, имеет асимптотическое направление.
Доказательство. Вектор  , коллинеарный ди-аметру, сопряжённому хордам, имеющим неасимпто-тическое направление
, коллинеарный ди-аметру, сопряжённому хордам, имеющим неасимпто-тическое направление  , имеет координаты:
, имеет координаты:
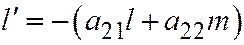 ,
, 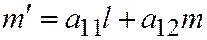 . Отсюда, в силу
. Отсюда, в силу 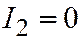 находим:
находим: 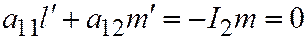 . (Проверим равенство
. (Проверим равенство 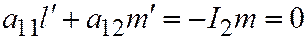 . Подставим
. Подставим 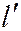 и
и 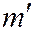 :
: 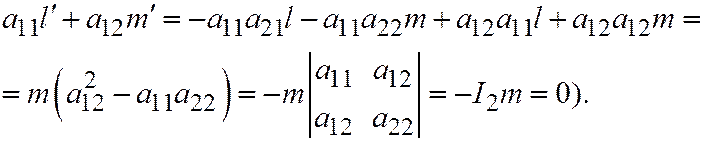
Аналогично 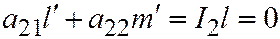 . Значит,
. Значит,
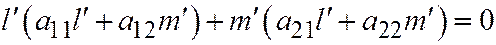 или
или
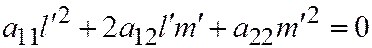 , т.е. вектор
, т.е. вектор  имеет асимптотическое направление. Теорема 4 доказана.
имеет асимптотическое направление. Теорема 4 доказана.
Замечание. Разделив обе части уравнения 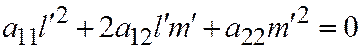 на
на 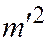 , получим квадратное уравнение:
, получим квадратное уравнение: 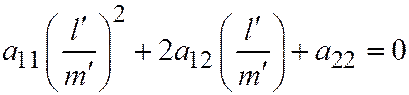 . Корни которого равны
. Корни которого равны 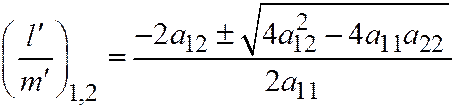 . В силу того, что дискриминант этого квадратного уравнения равен нулю, получаем, что вектор
. В силу того, что дискриминант этого квадратного уравнения равен нулю, получаем, что вектор  имеет асимптотическое направление. Аналогично, разделив уравнение
имеет асимптотическое направление. Аналогично, разделив уравнение 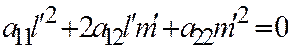
на 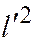 , получим, что вектор
, получим, что вектор 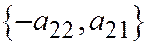 имеет асимптотическое направление. То есть векторы
имеет асимптотическое направление. То есть векторы  и
и 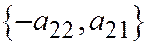 , по крайней мере один из которых ненулевой, имеет асимптотическое направле-ние для линии параболического типа.
, по крайней мере один из которых ненулевой, имеет асимптотическое направле-ние для линии параболического типа.
Теорема 5. Если линия - парабола, то диаметром является любая прямая, имеющая асимптотическое направление относительно этой линии.
Доказательство. Если линия является параболой, то на основании теоремы 4 все её диаметры имеют асимптотическое направление. Докажем, что и обратно: любая прямая 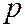 , имеющая асимптотическое направление параболы, является её диаметром.
, имеющая асимптотическое направление параболы, является её диаметром.
Возьмём на прямой 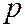 произвольную точку
произвольную точку 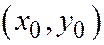 и выберем ненулевой вектор
и выберем ненулевой вектор  , не имеющий асимптотического направления, и такой, чтобы его координаты удовлетворяли соотношению:
, не имеющий асимптотического направления, и такой, чтобы его координаты удовлетворяли соотношению:
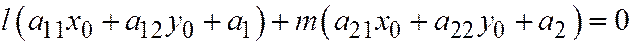 . Для этого достаточно положить
. Для этого достаточно положить 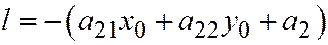 ,
,  . Вектор
. Вектор  ненулевой, т.к. для параболы, заданной общим уравнением, система:
ненулевой, т.к. для параболы, заданной общим уравнением, система: 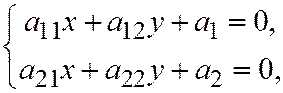 несовместна (это система для определения центра линии, а у параболы нет центра). А если система несовместна, то определитель её равен нулю (а он равен нулю, т.к. это
несовместна (это система для определения центра линии, а у параболы нет центра). А если система несовместна, то определитель её равен нулю (а он равен нулю, т.к. это 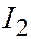 , а у параболы
, а у параболы 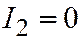 ), а ранг расширенной матрицы равен 2, поэтому али
), а ранг расширенной матрицы равен 2, поэтому али 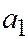 , или
, или  , не равны нулю, т.е. вектор
, не равны нулю, т.е. вектор  ненулевой.
ненулевой.
Далее, этот вектор  не имеет асимптотичес-кого направления, т.к. предполагая обратное, т.е.
не имеет асимптотичес-кого направления, т.к. предполагая обратное, т.е. 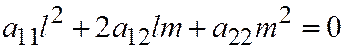 или
или
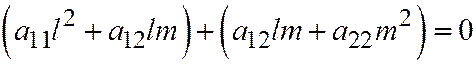 . Откуда:
. Откуда:
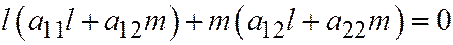 . Поскольку вектор
. Поскольку вектор  ненулевой, а определитель
ненулевой, а определитель 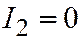 , то мы должны иметь
, то мы должны иметь 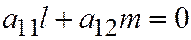 и
и 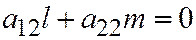 . Теперь в выражение
. Теперь в выражение 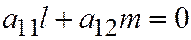 подставим значения
подставим значения 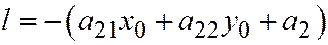 и
и  . Получим:
. Получим:
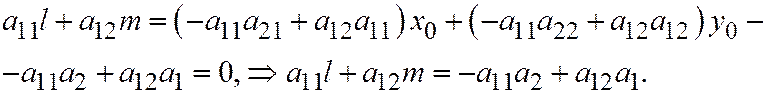
Аналогично 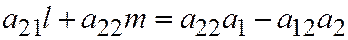 . Далее, рассмот-рим систему:
. Далее, рассмот-рим систему: 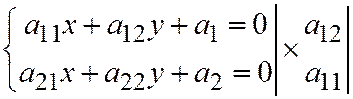 , умножаем:
, умножаем:  вычитаем:
вычитаем:
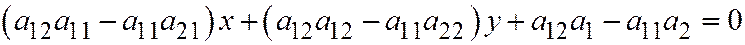 .
.
В этом уравнении 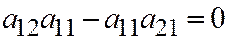 ,
,  ,
,
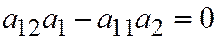 , т.е. все коэффициенты и свободный член равны нулю. Таким образом, предположив, что вектор
, т.е. все коэффициенты и свободный член равны нулю. Таким образом, предположив, что вектор  имеет асимптотическое направление, мы получили, что система
имеет асимптотическое направление, мы получили, что система 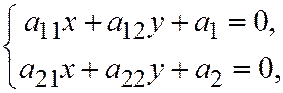 совместна, что для параболы невозможно.
совместна, что для параболы невозможно.
Значит, при указанном выборе  и
и 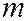 уравнение
уравнение 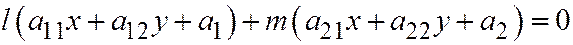 будет урав-нением прямой
будет урав-нением прямой 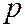 . Теорема 5 доказана.
. Теорема 5 доказана.
Замечание. Если линия имеет прямую центров, то каждая точка этой прямой должна принадлежать каждому из диаметров линии. Таким образом, прямая центров оказывается единственным диаметром линии; так как в рассматриваемом случае линия второго порядка есть пара параллельных (или совпадающих) прямых, а линия центров есть прямая линия, лежащая посередине между ними, то эта последняя прямая и будет единственным диаметром линии (распадающейся на две параллельные или совпадающие прямые).
II. Диаметры линий второго порядка, заданных каноническими уравнениями.
Если эллипс задан каноническим уравнением 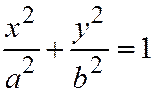 , то здесь
, то здесь 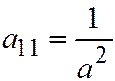 ,
, 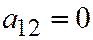 ,
, 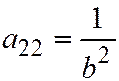 ,
,  , и уравнение диаметра
, и уравнение диаметра 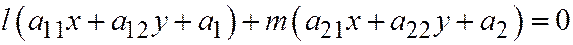 , сопряжённого хордам, параллельным ненулевому вектору
, сопряжённого хордам, параллельным ненулевому вектору  , будет иметь вид:
, будет иметь вид: 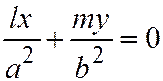 ; а уравнение диаметра, сопряженного с ним:
; а уравнение диаметра, сопряженного с ним: 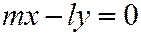 . Это из того, что хорды имеют направляющий вектор
. Это из того, что хорды имеют направляющий вектор  ; значит прямая с этим направляющим вектором должна иметь вид:
; значит прямая с этим направляющим вектором должна иметь вид: 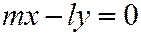 .
.
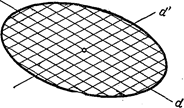
На рис. 216 изображён эллипс, два его сопряженных диаметра и хорды, параллельные каждому из них.
|
Рис. 216.
Если гипербола задана каноническим уравнением 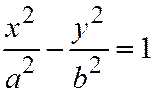 , то здесь
, то здесь 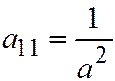 ,
, 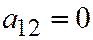 ,
, 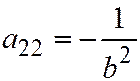 ,
,  , и уравнение диаметра
, и уравнение диаметра 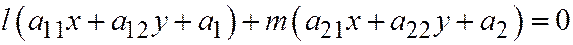 , сопряжённого хордам, параллельным ненулевому вектору
, сопряжённого хордам, параллельным ненулевому вектору  , не имеющему асимптотического направления (т.е. неколлинеарному ни одному из векторов
, не имеющему асимптотического направления (т.е. неколлинеарному ни одному из векторов 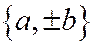 ), будет иметь вид:
), будет иметь вид: 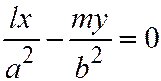 ; а уравнение диаметра, сопряженного с ним:
; а уравнение диаметра, сопряженного с ним: 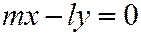 . Это из того, что хорды имеют направляющий вектор
. Это из того, что хорды имеют направляющий вектор  ; значит прямая с этим направляющим вектором должна иметь вид:
; значит прямая с этим направляющим вектором должна иметь вид: 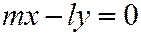 .
.
На рис. 217 изображена гипербола, два её сопряженных диаметра и хорды, параллельные каждому из них.

Рис. 217.
Уравнение диаметра параболы 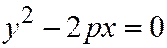 , сопряженного хордам, параллельным ненулевому вектору
, сопряженного хордам, параллельным ненулевому вектору  имеет вид:
имеет вид:  , ил
, ил 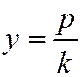 , где
, где 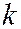 - угловой коэффициент хорд. Все диаметры параболы параллельны её оси. На рис. 218 дано одно из семейств параллельных хорд и сопряженный им диаметр.
- угловой коэффициент хорд. Все диаметры параболы параллельны её оси. На рис. 218 дано одно из семейств параллельных хорд и сопряженный им диаметр.

|
Рис. 218.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1786; Нарушение авторских прав?; Мы поможем в написании вашей работы!