Электромагнитных систем

В магнитных и электромеханических элементах, обтекаемых постоянным током, тепло выделяется только в тех элементах, в которых непосредственно протекает ток (катушках, резисторах, контактах, монтажных проводах и т. д.). В элементах, обтекаемых переменным током или подверженных воздействию импульсов тока, необходимо также учитывать потери в магнитопроводе за счет гистерезиса и вихревых токов, а также потери в проводящих контурах, связанных с изменяющимися магнитными потоками. Потери в токоведущих частях определяются по закону Ленца - Джоуля. Потери в магнитопроводах лучше всего определять на основании опытных данных. Для сердечников, шихтованных из листовой стали и пермаллоя, в стандартах на эти материалы и литературе приводят удельные потери при фиксированных значениях индукции и частоты. Для значений индукции и частоты, не очень сильно отличающихся от справочных, пересчёт можно производить по формулам

, .

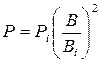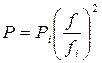Здесь 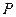,,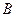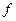- определяемые удельные потери при данных индукции и частоте;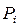,,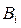 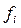- те же величины по справочным данным.

При определении потерь необходимо помнить, что они сильно зависят от технологии изготовления и сборки магнитопроводов. Для материалов, имеющих текстуру, они зависят также от направления намагничивания.

Часть тепла, выделяемого в некотором элементе, может идти на его нагрев, остальное – отдаваться в окружающую среду.

Известно, что характеристики электротехнических устройств и особенно элементов, применяемых в автоматике, сильно зависят от температуры. Например, медные и алюминиевые провода при изменении температуры на 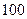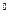С, изменяют своё электрическое сопротивление примерно на 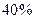. С изменением температуры значительно изменяются характеристики полупроводниковых приборов. При температуре свыше 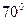¸ 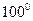С германиевые приборы, а при 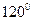¸ 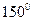С и выше кремневые – выходят из строя.

Срок службы изоляции сильно зависит от температуры. Так при повышении температуры на 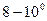по сравнению с предельно допустимой, срок службы изоляции сокращается примерно вдвое. При температуре 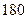¸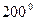С органическая изоляция обугливается и приходит в негодность. Отдача тепла в окружающую среду может происходить тремя способами.

Теплопроводность – процесс распространения тепла от более нагретых элементов к менее нагретым, приводящий к выравниванию температур. В чистом виде теплопроводность протекает только в твёрдых телах. Интенсивность передачи тепла при теплопроводности определяется градиентом температуры и свойствами вещества, характеризуемыми коэффициентом теплопроводности 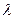. Как правило, вещества, обладающие высокой электропроводимостью, обладают и высокой теплопроводностью и наоборот. Наибольшее значение коэффициента теплопроводности имеют металлы серебро и медь:

; .

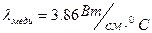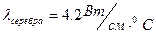Для сравнения укажем, что теплопроводность стекла порядка 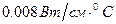, гетинакса - 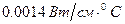и т. д.

Конвекция – перенос тепла в жидких и газообразных средах (при определённых условиях и в сыпучих) за счёт движения частичек среды. Конвекция обычно сочетается с теплопроводностью. При этом имеет место конвективный теплообмен. Различают естественную конвекцию, когда перемещение среды происходит за счёт неоднородной плотности, обусловленной неоднородной температурой, и искусственную конвекцию, обусловленную принудительным движением среды, например, вызванную работой вентилятора. Интенсивность отвода тепла при конвективном теплообмене зависит от физических свойств среды (теплоёмкость, теплопроводность, вязкость, плотность), от формы и размеров теплоотдающей поверхности и её состояния (гладкая, шероховатая). Законы теплоотдачи при конвекции очень сложны и расчёт в этом случае ведётся преимущественно на основании опытных данных, обобщённых в виде критериальных зависимостей, построенных методами теории подобия. Критериями подобия называют безразмерные комбинации из параметров и переменных величин, характеризующих данный процесс или явление.

Лучистый теплообмен – перенос тепла электромагнитными колебаниями (лучеиспусканием). Лучистый теплообмен между двумя телами зависит от четвёртой степени разности температур их поверхностей, от состояния их поверхностей (цвет, степень шероховатости), от их взаимного расположения и размеров. Подробно вопросы теплоотдачи рассматриваются в специальных курсах.

В электрических расчётах для относительно узкого диапазона температур при определении теплоотдачи с поверхности устройства в окружающую газообразную или жидкую среду обычно используют формулу Ньютона

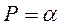
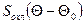(1.1)

здесь 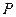- мощность, отдаваемая охлаждаемой поверхностью в окружающую среду; 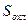- величина охлаждаемой поверхности; 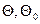- температуры, соответственно, теплоотдающей поверхности и окружающей среды; 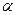- коэффициент теплоотдачи, численно равный мощности, отдаваемой с единицы поверхности в окружающую среду при разности температур между ними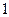 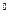С. Величина коэффициента теплоотдачи зависит от всех факторов, определяющих процессы конвективного и лучистого теплообмена. Его значение чаще всего определяют опытным путём. Для того, чтобы получить удовлетворительные результаты расчёта по формуле Ньютона, условия, для которых производится расчёт, должны быть близки к условиям, при которых определяется коэффициент теплоотдачи.

При тепловых расчётах различают три вида тепловых режимов: длительный, кратковременный и повторно-кратковременный. Особенности этих режимов удобно рассмотреть на примере анализа процессов нагрева и охлаждения идеализированного однородного тела. Идеализация заключается в том, что принимают в любой момент времени одинаковую температуру любых точек тела. Это равносильно предположению, что вещество тела обладает бесконечно большой теплопроводностью. Предполагают также, что условия теплоотдачи со всех элементов поверхности тела одинаковы. При указанных допущениях, используя формулу Ньютона, можно записать следующее уравнение теплового баланса тела:

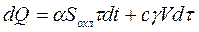(1.2)

Здесь 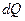- количество тепла, подводимое к телу за время 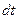; 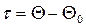- превышение температуры тела над окружающей средой, называемое часто ²перегревом², 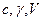- теплоёмкость, плотность и объём тела. Первый член правой части определяет количество тепла, которое отдаёт тело в окружающее пространство за время 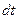, а второй – количество тепла, которое за это же время пошло на нагрев тела, т. е. на повышение его температуры.

Выражение (1.2) удобно переписать, разделив все его члены на ,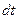

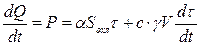. (1.3)

Дифференциальное уравнение (1.3) – линейное, первого порядка с постоянными коэффициентами. Его решение может быть записано в виде

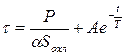. (1.4)

Здесь - постоянная интегрирования, 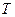- постоянная времени нагрева.

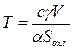. (1.5)

Постоянную интегрирования определим из условия, что при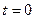

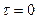
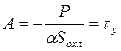, (1.6)

где 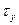- превышение температуры тела, при которой всё тепло, подводимое к нему, будет отдаваться в окружающую среду. Подставляя значение в равенство (1.4), получим уравнение нагрева однородного тела

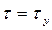
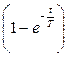. (1.7)

Для того, чтобы получить уравнение охлаждения однородного тела, положим в уравнении (1.3) 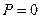, т.е. примем, что к телу не подводится энергия. В этом случае получим однородное линейное дифференциальное уравнение первого порядка, решение которого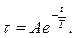

При 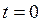, , 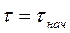т. е. перегреву в момент начала процесса охлаждения. Соответственно 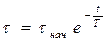, (1.8)

Имея уравнение нагрева и охлаждения, рассмотрим тепловые режимы.

Кратковременный режим характеризуется тем, что t <<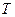.При этом условии в формуле (1.7) разложим 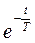в степенной ряд и ограничимся первыми членами разложения 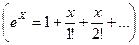, т.е.

.

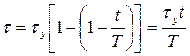Подставляя в последнее выражение значение 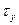из уравнения (1.6) и 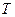из уравнения (1.5), получим 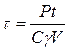. (1.9)

Из формулы (1.9) видно, что при кратковременном режиме теплоотдачей в окружающее пространство можно пренебречь и считать, что вся подводимая к телу энергия идет на его нагрев.

Таким образом, кратковременный режим можно определить как такой, при котором практически вся подводимая к телу энергия идёт на его нагрев, а при выключении тело успевает остыть до температуры окружающей среды (рис.1.1а). Теоретически, чтобы это произошло, время паузы должно равняться бесконечности. Однако, если считать, что перегревом, составляющим несколько процентов от начального, можно пренебречь, то можно принять, что тело остывает до температуры окружающей среды за 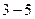постоянных времени (; ; ; ; ).

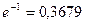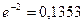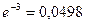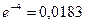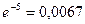Длительный режим характеризуется тем, что температура тела достигает установившегося значения, при котором всё тепло, подводимое к телу, отдаётся в окружающую среду. Также как и для остывания, в зависимости от требуемой точности, можно принять, что установившийся режим наступает через 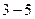постоянных времени нагрева(рис.1.1).

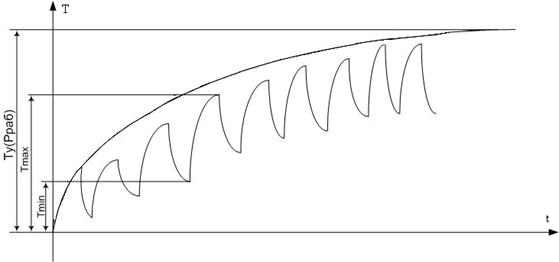
Рис.1.1

Повторно – кратковременный режим характеризуется тем, что за время работы t_p тело не успевает нагреться до установившейся температуры 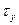, а за время паузы t_п не успевает остыть до температуры окружающей среды (рис.1.1).

Рассмотрим простейший случай, когда время работы 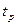и время паузы 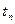имеют постоянные значения, т. е. имеет место установившийся цикл. Время цикла

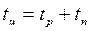. (1.10)

Если цикл повторяется многократно и мощность за время работы в каждом цикле постоянна, то наступает квазиустановившийся режим, при котором превышение температуры тела колеблется от 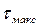до 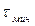(рис. 1).

Закон изменения температуры в процессе работы можно определить, исходя из формулы (1.4), но теперь при 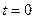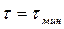, соответственно, постоянная интегрирования

.

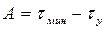Подставляя новое значение в формулу (1.4), получим

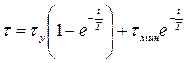. (1.11)

В свою очередь, используя формулу (1.8), 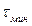можно выразить через:

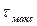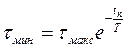. (1.12)

Положим в формуле (1.11)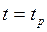, соответственно. 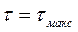Используя при этом формулу (1.12), получим

.

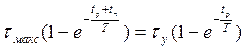Откуда с учётом формулы (1.10) следует

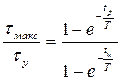. (1.13)

Есл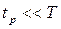и и 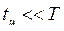, то раскладывая 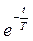в степенной ряд и ограничиваясь первыми членами разложения, получим

.

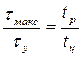Выражая 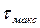и 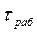с помощью формулы Ньютона (1.1) и приняв, что 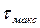соответствует длительно допустимому перегреву и соответственно длительно допустимой мощности (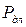), окончательно найдём

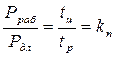, (1.14)

где 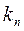- коэффициент перегрузки, показывающий, во сколько раз мощность 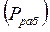, допустимая в течение работы при повторно- кратковременном режиме, больше мощности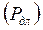длительно допустимого режима. Величину, обратную 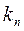, определяют как отношение времени работы ко времени цикла и называют относительной продолжительностью включения 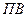, обычно выражаемую в процентах,

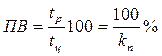. (1.15)

Очевидно, что если коэффициент перегрузки по мощности 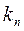, то коэффициент перегрузки по току 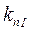равен корню квадратному из коэффициента перегрузки по мощности

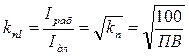. (1.16)

В реальных телах (катушках в магнитных системах и т. д.) вследствие их неоднородности процессы нагрева и охлаждения протекают сложней чем в идеализированном однородном теле. Кривые нагрева и охлаждения уже не будут экспонентами и понятие постоянной времени, строго говоря, для них не имеет смысла. Однако приведённые определения тепловых режимов остаются в силе и в этом случае. При этом постоянную времени принимают равной времени, в течение которого средняя температура тела изменится в 1/e раз, т.е.примерно на 63 %. Таким образом, однородное тело - это упрощённая модель реальных тел. На этой модели легче выявить характерные особенности тепловых режимов.

Дата добавления: 2014-01-04