Задачи и упражнения. Теоретические вопросы, выносимые на экзамен:

Теоретические вопросы, выносимые на экзамен:

Рекомендуется изучить самостоятельно:

Ø [2] – стр. 64 — 74;

Ø [3] – стр. 116 — 127.

1. Функция распределения случайной величины. Свойства функции распределения.

2. Плотность распределения вероятностей случайной величины. Свойства плотности распределения.

3. Основные непрерывные случайные величины. Свойство отсутствие последействия.

10.8. В результате успешного усвоения материала лекции студент должен знать:

ü определения:

Ø функции распределения случайной величины;

Ø плотности распределения случайной величины;

Ø абсолютно непрерывной случайной величины;

Ø сингулярной случайной величины;

Ø равномерной случайной величины;

Ø нормальной случайной величины;

Ø показательной случайной величины;

Ø распределения Коши;

Ø распределения Лапласа;

ü свойства:

Ø функции распределения случайной величины;

Ø плотности распределения случайной величины;

ü теоремы:

Ø о необходимых и достаточных условиях функции распределения;

Ø о необходимых и достаточных условиях плотности распределения;

Ø Лебега о разложении функции распределения;

Ø о функциях от случайных величин;

уметь:

ü доказывать свойства:

Ø функции распределения случайной величины;

Ø плотности распределения случайной величины.

1. Случайная величина 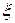имеет функцию распределения

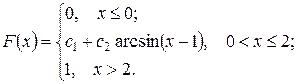
Найти: а) константы 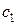и 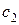; б) плотность распределения 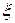; в) вероятность 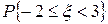; г) вероятность.

2. Случайная величина 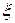имеет функцию распределения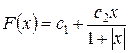

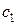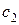Найти: а) константы и ; б) плотность распределения ; в) .

3. Плотность распределения случайной величины 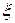определена соотношением:

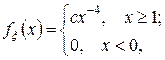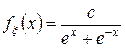а) б) , в) .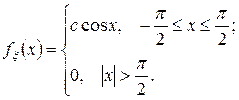

Найти постоянную 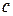и функцию распределения случайной величины .

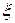4. Случайная величина 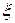имеет показательное распределение с параметром . Найти распределение случайных величин:

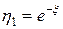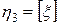а) ; б) ; в) — дробная часть; г) — целая часть.

5. Случайная величина 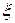имеет равномерное распределение на отрезке 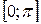. Найти распределение случайной величины .

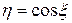6. Случайная величина 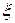имеет равномерное распределение на отрезке . Найти распределение случайной величины .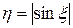

[1] Лебег Анри Леон (Lebesgue Henri Léon) (28.06.1875–26.07.1941) — французский математик, иностранный член–корреспондент АН СССР (1929), член Парижской академии наук (1922). Профессор парижского университета (1910). Один из основателей современной теории функций действительного переменного. Главная заслуга создание теории меры (мера Лебега) и обобщение понятия интеграла (интеграл Лебега).

[2] Коши Огюсте Луи (Cauchy Augustin Louis) (21.08.1789–23.05.1857) — французский математик, иностранный почетный член Петербургской АН (1831), Парижской АН (1816). Труды относятся к различным областям математики, преимущественно к математическому анализу и математической физике.

Дата добавления: 2014-01-04