Метрика пространства признаков

ДИАГНОСТИКА ПО РАССТОЯНИЮ В ПРОСТРАНСТВЕ ПРИЗНАКОВ

МЕТРИКА ПРОСТРАНСТВА ПРИЗНАКОВ

План лекции

Анализ и проверка домашней работы

Организационный момент.

Ход лекции.

3. Ответьте на вопросы:

1. На чем основаны методы разделения в пространстве призна­ков?

2. Опишите пространство признаков. Чем эта система может быть охарактеризована?

3. В чем состоит условие компактности?

4. Дайте пояснение линейному методу разделения.

5. Приведите достаточное условие линейной раз­делимости двух непересекающихся областей. Приведите пример.

6. В каком случае может быть построена разделяющая функция?

7. Опишите метод трубок, который дает некоторые правила, с помощью которых можно образовать диагностически ценные комплексы признаков.

8. Поясните физический смысл метода потенциалов.

1.1 Координаты пространства.

1.2 Евклидово расстояние между точками.

1.3 Диагностическая мера расстояния.

1.4 Метрика в неизотропном пространстве признаков.

1.5 Обобщенная метрика пространства признаков

1.6 Замечание о классификации пространства признаков.

2.1 Выбор эталона.

2.2 Алгоритм распознавания.

2.3 Надежность распознавания.

2.4 Замечания о выборе метрики.

2.5 Диагностика по угловому расстоянию.

2.6 Диагностика по расстоянию до множества.

2.7 Алгоритм распознавания по методу среднего расстояния.

2.8 Метод минимального расстояния до множества.

В большинстве методов распознавания делается естественное предположение, что изображения объектов одного класса (образа) более близки друг другу, чем изображения разных классов. Метрические методы основаны на количественной оценке этой близости. В качестве изображения объекта принима­ется точка в пространстве признаков, мерой близости считается расстояние между точками.

1.1 Координаты пространства. Как известно, в пространстве признаков объект характеризуется N-мерным вектором

x = (x_1, x₂,...,x_N). (11.1)

Координаты пространства Xj могут быть непрерывными или дис­кретными величинами. В последнем случае x_J представляет приз­нак k_r имеющий несколько диагностических разрядов. Часто используется кодирование признаков в бинарном коде. Тогда ко­ордината Xj выражается двоичным числом и может иметь значе­ния: X_j1 = О, X_j2 = 1. При использовании унитарного (двоичного) кода возможные значения таковы: x_j1 = —1, x_j2 = 1.

В диагностическом пространстве объект описывается вектором, размерность которого может отличаться от размерности вектора в пространстве признаков. В качестве координат диагностического пространства принимаются функции

(11. 2)

В дальнейшем для простоты рассматриваются метрические методы в пространстве признаков, но все результаты легко пере­носятся на диагностическое пространство.

1.2 Евклидово расстояние между точками. Обычное расстояние между точками х и а пространства признаков

Равенство (11.3) устанавливает метрику евклидова простран­ства, причем основные метрические свойства этого пространства выражаются условиями:

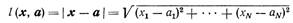
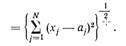(11.4)

В задачах распознавания часто удобно в качестве меры рассто­яния принимать квадрат расстояния

Величина L² тесно связана с многомерным нормальным распре­делением, более проста для вычислений, а неравенство

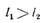(11.6)

влечет за собой более сильное неравенство

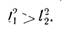(11.7)

В некоторых случаях применяют термин ОБОБЩЕННОЕ ПРОСТРАНСТВО - Обобщенное расстояние удов­летворяет метрическим свойствам (11.4) евклидова пространства.

1.3 Диагностическая мера расстояния. Иногда оказывается целе­сообразным использовать в качестве диагностической меры рас­стояния некоторую степень расстояния

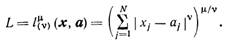(11.9)

В дальнейшем будем часто использовать квадратичное (ев­клидово) расстояние (v = 2) и вторую степень расстояния. Тогда диагностическая мера расстояния между точками х и а

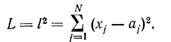(11.11)

1.4 Метрика в неизотропном пространстве признаков. Предыдущие определения расстояния соответствовали однородному, изотроп­ному пространству признаков, координаты которого имеют об­щую единицу измерений. Такое пространство однородных приз­наков используется в ряде задач распознавания Например, для акустической диагностики в качестве признаков могут применяться амплитуды соответствующих гармоник и т. п.

Диагностика с помощью признаков в двоичном коде соответ­ствует использованию изотропного, однородного пространства признаков. Однако во многих задачах диагностики пространство признаков является анизотропным, т. е. единицы измерения в раз­личных направлениях различны. Координатам x_J могут соответ­ствовать параметры различной физической природы (например, x₁ — температура_; х₂— давление и т. п.).

С помощью компонентов весового вектора

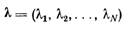
можно учесть различную диагностическую ценность признаков, придавая большее значение наиболее значимым признакам. Так как для диагностики важен относительный вес, то можно использовать условие нормирования в виде

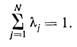(11.13)

Введение весовых коэффициентов деформирует пространство признаков.

1.5 Обобщенная метрика пространства признаков. Соотноше­ние (11.11)устанавливает «неравноправие» отдельных координат в пространстве признаков, но оно не учитывает роль координаты Xj-для диагноза Dj. Диагностическое значение признаков различно для различных диагнозов и расстояние точки х до точки a при­надлежащей диагнозу D

Для непрерывно распределенных признаков х_J вероятность диск­ретных значений заменяется плотностью вероятности, суммирова­ние— интегрированием по области значений х_J.

1.6 Замечание о классификации пространства признаков. В зави­симости от используемой метрики, будем различать три вида пространства признаков.

Неизотропное, неоднородное пространство соответствует ме­трике общего вида . Если для всех диагнозов

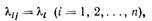(11.21)

то пространство называется однородным, неизотропным. Нако­нец, при

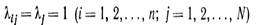(11.22)

пространство считается однородным и изотропным.

Дата добавления: 2014-01-04