Сдвиг и вращение вокруг произвольной точки

Ну а теперь перейдем к самому общему случаю: вращению вокруг произвольного центра со сдвигом:

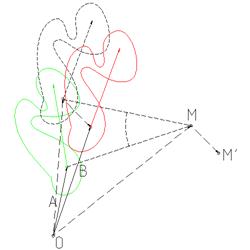
Вращение вокруг произвольной точки M с последующим сдвигом

Теперь к произведению матриц слева необходимо добавить еще один сдвиг (на вектор MM'). После выполнения умножения мы получим ту же самую матрицу, что получили в предыдущем пункте, но смещение теперь будет суммарным, как если бы мы вращали объект вокруг нового центра, который получается путем смещения оригинального центра вращения на вектор MM'.

Решая аналогичную предыдущему пункту систему уравнений, получим значение угла поворота и сумму радиус-вектора центра вращения и вектора смещения изображения. Если анализировать большое количество изображений, для которых смещения являются небольшими и случайными, а центр вращения остается в одном и том же месте, то, например, медианным усреднением набора полученных векторов можно определить радиус-вектор центра вращения, близкий к реальному с точностью, которая будет тем лучше, чем больше наблюдений мы сделали и чем выше точность определения координат объектов.

Ну, а в следующей заметке я попытаюсь применить изложенное для автоматического определения центра вращения поля и его смещения от кадра к кадру.

36. Жёсткие преобразования изображений. Оптимизация симплекс-методом.

http://www.bsu.by/Cache/Page/353423.pdf

Подмножество

аффинных преобразований - перенос, поворот и отражение

называются жёсткими преобразованиями, так как в процессе

их выполнения сохраняются расстояния и углы между любыми

двумя точками преобразуемой фигуры.

http://mm.lti-gti.ru/works_lectures/6.htm

http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%BF%D0%BB%D0%B5%D0%BA%D1%81-%D0%BC%D0%B5%D1%82%D0%BE%D0%B4

Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан советским математиком Канторовичем Л. В. в 1937 году.

Содержание [убрать] · 1 Описание · 2 Алгоритм симплекс-метода o 2.1 Усиленная постановка задачи o 2.2 Алгоритм · 3 Двухфазный симплекс-метод o 3.1 Причины использования o 3.2 Модификация ограничений § 3.2.1 Различия между дополнительными и вспомогательными переменными o 3.3 Фазы решения · 4 Модифицированный симплекс-метод · 5 Мультипликативный вариант симплекс-метода · 6 Другие варианты симплекс-метода · 7 Двойственный симплекс-метод · 8 Вычислительная эффективность · 9 Примечания · 10 Литература · 11 Ссылки

[править]Описание

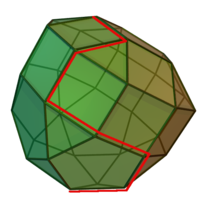
Переход от одной вершины к другой

Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.

Заметим, что каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным комплексом. Уравнение W (x) = c, где W (x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k -мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.

Последовательность вычислений симплекс-методом можно разделить на две основные фазы:

1. нахождение исходной вершины множества допустимых решений,

2. последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.

При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, скорее всего, далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод, соответственно, делится на однофазный и двухфазный.

[править]Алгоритм симплекс-метода

[править]Усиленная постановка задачи

Рассмотрим следующую задачу линейного программирования:

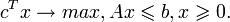
Теперь поставим эту задачу в эквивалентной усиленной форме. Необходимо максимизировать Z, где:

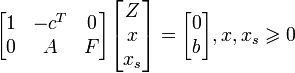
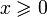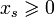Здесь x — переменные из исходного линейного функционала, x _s — новые переменные, дополняющие старые таким образом, что неравенство переходит в равенство, c — коэффициенты исходного линейного функционала, Z — переменная, которую необходимо максимизировать. Полупространства и в пересечении образуют многогранник, представляющий множество допустимых решений. Разница между числом переменных и уравнений даёт нам число степеней свободы. Проще говоря, если мы рассматриваем вершину многогранника, то это число рёбер, по которым мы можем продолжать движение. Тогда мы можем присвоить этому числу переменных значение 0 и назвать их «непростыми». Остальные переменные при этом будут вычисляться однозначно и называться «простыми». Полученная точка будет вершиной в пересечении соответствующих непростым переменным гиперплоскостей. Для того, чтобы найти т. н. начальное допустимое решение (вершину, из которой мы начнём движение), присвоим всем изначальным переменным x значение 0 и будем их считать непростыми, а все новые будем считать простыми. При этом начальное допустимое решение вычисляется однозначно: .

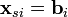[править]Алгоритм

Теперь приведём шаги алгоритма. На каждом шаге мы будем менять множества простых и непростых векторов (двигаться по рёбрам), и матрица будет иметь следующий вид:

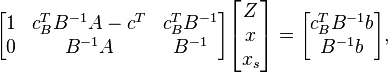
где c _B — коэффициенты вектора c соответствующие простым переменным (переменным x _s соответствуют 0), B — столбцы 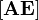, соответствующие простым переменным. Матрицу, образованную оставшимися столбцами обозначим D. Почему матрица будет иметь такой вид поясним в описании шагов алгоритма.

Первый шаг.

Выбираем начальное допустимое значение, как указано выше. На первом шаге B — единичная матрица, так как простыми переменными являются x _s. c _B — нулевой вектор по тем же причинам.

Дата добавления: 2014-01-04