Теорема Карунена — Лоэва

[править]

Материал из Википедии — свободной энциклопедии

Эта статья или раздел — грубый перевод статьи на другом языке (см. Проверка переводов). Он мог быть сгенерированпрограммой-переводчиком или сделан человеком со слабыми познаниями в языке оригинала. Вы можете помочь улучшить перевод. Оригинал можно найти слева в списке «на других языках». Статья, целиком являющаяся машинным переводом, может быть удалена на основании критерия быстрого удаления С2.

В теории случайных процессов теорема Карунена-Лоэва (названа в честь Кари Карунена и Мишеля Лоэва) — представление случайного процесса в виде бесконечной линейной комбинации ортогональных функций, аналогичное представлению рядов Фурье — последовательному представлению функций на ограниченном интервале. В отличие от рядов Фурье, где коэффициенты являются действительными числами и базис представления состоит из синусоидальных функций (то есть, из функций синус и косинус с разными частотами), коэффициенты в теореме Карунена-Лоэва — случайные переменные, и базис представления зависит от процесса. Ортогональные базисные функции, использованные в этом представлении, определяет функция ковариации процесса. Если мы рассматриваем стохастический процесс как случайную функцию F, то есть процесс, в котором функция на интервале [ a, b ] принимает значение F, то эта теорема может рассматриваться как случайное ортонормальное расширение F.

Центрированный случайный процесс { X _t } _{t ∈ [ a, b ]} (где центрирование означает, что математические ожидания E(X _t) существуют и равны нулю для всех значений параметра t из [ a, b ]), удовлетворяющий техническому условию непрерывности, допускает разложение следующего вида:

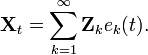
где Z _k — взаимнонекоррелированые случайные величины и функции e_k — непрерывные вещественные функции на [ a, b ], ортогональные в L ² [ a, b ]. В случае нецентрированного процесса имеет место аналогичное разложение, получаемое разложением функции математического ожидания в базисе e_k.

Если процесс 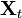гауссовский, то случайные величины Z _k — тоже гауссовские и являются независимыми. Этот результат обобщает преобразования Карунена-Лоэва. Важным примером центрированного случайного процесса на интервале [0,1] является винеровский процесс, и теорема Карунена-Лоэва может быть использована для получения канонического ортогонального представления. В этом случае разложение состоит из синусоидальных функций.

Приведенные выше разложения в также известны как разложения или декомпозиция Карунена-Лоэва (эмпирическая версия, то есть, с коэффициентами из исходных числовых данных), как анализ главных компонент, собственное ортогональное разложение или преобразование Хотеллинга.

Содержание [убрать] · 1 Формулировка o 1.1 Статистики второго порядка · 2 Формулировка теоремы o 2.1 Суммы Коши o 2.2 Особый случай: гауссовское распределение · 3 Процесс Винера · 4 Использование · 5 См. также · 6 Ссылки

[править]Формулировка

Сформулируем результат в терминах комплекснозначных стохастических процессов. Результаты могут быть применены к вещественнозначным процессам без модификаций, вспоминая, что число, комплексно-сопряженное с действительным числом, совпадает с ним самим.

Для случайных элементов X и Y скалярное произведение определяется формулой

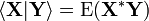
где * обозначает операцию комплексного сопряжения.

[править]Статистики второго порядка

Скалярное произведение корректно определено, если как 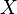, так и имеют конечные вторые моменты, или, что то же самое, если они оба квадратично интегрируемы. Отметим, что скалярное произведение связано с ковариацией и корреляцией. В частности, для случайных переменных со средним нулевым значением, ковариация и скалярное произведение совпадают. Функция автоковариации

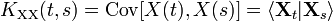
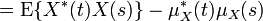
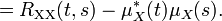
Если процесс { X _t } _t центрированный, то

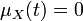
для всех t. Таким образом, автоковариация K _XX равна автокорреляции R _XX:

Отметим, что если { X _t } _t центрированный и t ₁, ≤ t ₂, …, ≤ t_N являются точками на интервале [ a, b ], следовательно

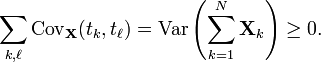
[править]Формулировка теоремы

Теорема. Рассмотрим центрированный случайный процесс { X _t } _t, индексированный t на интервале [ a, b ] с ковариационной функцией Cov _X. Предположим, что ковариационная функция Cov _X (t, s) непрерывна по совокупности переменных t, s. Тогда Cov _X — положительно определенное ядро, и по теореме Мерсера интегральный оператор T в L²[ a, b ] (близкой к мере Лебега на [ a, b ]) имеет ортонормированный базис из собственных векторов. Пусть { e_i } _i являются собственными векторами T, соответствующими ненулевым собственным значениям и

Тогда Z _i — центрированные ортогональные случайные величины и

ряд сходится в среднем квадратичном, а также равномерно по t. Кроме того

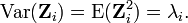
где 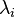собственное значение, соответствующее собственному вектору .

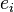[править]Суммы Коши

В формулировке теоремы интеграл в определении 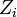можно понимать как предел в среднем сумм Коши случайных величин

где

[править]Особый случай: гауссовское распределение

Так как предел в среднем квадратичном из совместно гауссовских случайных величин является гауссовским и совместно гауссовские случайные (центрированные) величины независимы тогда и только тогда, когда они являются ортогональными, мы можем также заключить:

Теорема. Случайные величины Z _i имеют гауссовское распределение и являются независимыми, если первоначальный процесс { X _t } _t тоже является гауссовским.

В гауссовском случае, поскольку случайные величины Z _i являются независимыми, мы можем быть уверены в том, что:

почти наверное.

Отметим, что обобщая теорему Мерсера, мы можем заменить интервал [ a, b ] другими компактными пространствами C, а меру Лебега на [ a, b ] — борелевской мерой с носителем в C.

[править]Процесс Винера

Винеровский процесс в теории случайных процессов — это математическая модель броуновского движения или случайного блуждания с непрерывным временем. Здесь мы определяем его как центрированный гауссовский процесс B (t) с ковариационной функцией

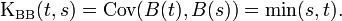
Легко видеть, что собственные векторы ковариации равны

а соответствующие собственные значения

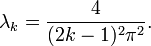
Это позволяет получить нам следующее представление винеровского процесса:

Теорема. Существует последовательность { W _i } _i независимых гауссовких случайных величин с нулевым средним и единичной дисперсией такая, что

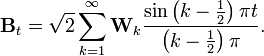
Сходимость является равномерной по t в норме L² так, что

равномерно по t.

[править]Использование

Было высказано мнение, что в проекте SETI, следует использовать преобразования Карунена-Лоэва для обнаружения сигналов с очень широким спектром. Аналогично, в системах адаптивной оптики иногда используют функции Карунена-Лоэва для восстановления информации о фазе фронта волны. (Dai 1996, JOSA A).

41. Искусственная нейронная сеть. Искусственный персептрон.

http://ru.wikipedia.org/wiki/%D0%98%D1%81%D0%BA%D1%83%D1%81%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BD%D0%B5%D0%B9%D1%80%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%81%D0%B5%D1%82%D1%8C

http://habrahabr.ru/post/134998/

http://www.victoria.lviv.ua/html/oio/html/theme5_rus.htm

http://neuronets.chat.ru/foundations.html

Дата добавления: 2014-01-04