Определение важности параметров средств защиты информации

Определение коэффициентов важности можно выполнить с применением математической теории измерений. В теории измерения различаются два класса и несколько подклассов измерений, как это показано на рисунке 9.2.

Воспользуемся для определения весов важности ЧПК СЗИ методом Саати, который относится согласно приведенной классификации к методу попарных сравнений.

Метод Саати заключается в следующем.

Предположим, что результаты попарного сравнения параметров описываются отношениями их весов, т.е. представимы в виде матрицы А (матрицы Саати):

. (9.4)

Справедливо следующее равенство:

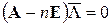, (9.5)

где Е - единичная матрица; - вектор весов.

Для нахождения вектора весов необходимо решить уравнение (9.5). Поскольку ранг матрицы равен 1, то n – единственное собственное число этой матрицы и, следовательно, уравнение (9.5) имеет ненулевое решение. Более того, это единственное решение, обладающее свойством

. (9.6)

Это решение и есть искомый вектор относительных весов параметров - вектор Саати.

Рассмотрим применение данного метода на гипотетическом примере. Пусть имеются следующие ЧПК СЗИ:

С – стоимость;

П – снижение производительности системы за счет его применения;

З – защищенность;

О – требуемый объем памяти.

Выполним попарное сравнение данных ЧПК. Саати предожил использовать шкалу следующего типа:

1-равная важность критериев;

3-умеренное превосходство одного критерия над другим;

5-существенное превосходство одного критерия над другим;

7-значительное превосходство одного критерия над другим;

9-очень сильное превосходство одного критерия над другим.

В принципе можно разрешить использовать любые соотношения типа «в N раз больше» Эксперта просят попарно сравнить ЧПК. Результат парных сравнений записывается в таблицу (табл.9.1).

Табл. 9.1

	С	П	З	О
С	1/1	3/1	1/1	8/1
П	1/3	1/1	1/3	3/1
З	1/1	3/1	1/1	7/1
О	1/8	1/3	1/7	1/1

Табл. 9.1. Предпочтения эксперта при попарном сравнении ЧПК

Простые дроби в клетках трактуются следующим образом. Например, на пересечении строки «Стоимость» и столбца «Производительность» записана дробь 7/1. Это выражает мнение эксперта о том, что важность ЧПК «Стоимость» в 7 раз выше, чем «Производительности». Далее простые дроби переводятся в десятичные и подсчитываются строчные суммы. Получается следующая таблица (табл.9.2).

Табл. 9.2

	С	П	З	О	Сумма по строке	Норм. сумма
С		0,33			10,33	0,374
П	0,33		0,33		4,66	0,169
З						0,435
О	0,125	0,33	0,143		0,6	0,022
				Сумма	27,6	1,00

Табл. 9.2. Предпочтения эксперта при попарном сравнении ЧПК

Правый столбец таблицы 9.2 получается в результате нормирования сумм по строке таким образом, чтобы их сумма в свою очередь была равна 1. Для этого разделим сумму каждой строки на 27,6 (сумма последнего столбца, т.е. сумма самих строчных сумм).

В результате нормировки получаем оценки важности для всех ЧПК. Отметим, что полученные оценки отражают исключительно точку зрения конкретного эксперта. На самом деле, вместо строчных сумм Саати рекомендует использовать собственный вектор матрицы парных сравнений, считая его более точной оценкой. Строчные суммы также допустимы, но, с точки зрения Саати, менее точны.

После определения весов ЧПК СЗИ осуществляется решение задачи комбинаторного перебора вариантов возможных решений, формируемых по входной матрице всех допустимых вариантов защиты. При этом решается задача многокритериальной оптимизации. Существует множество способов ее решения.

Дата добавления: 2014-01-04