Основные показатели изменения уровней временных рядов

Для характеристики развития явления во времени применяют следующие показатели:

· абсолютные приросты ;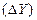

· темп роста (Т _р);

· темп прироста ();

· абсолютное ускорение или замедление ();

· относительное ускорение ( Т _р).

Абсолютный прирост уровней ряда рассчитывается как разность двух уровней. Он показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода.

В зависимости от базы сравнения абсолютные приросты могут быть цепными и базисными:

,

.

Взаимосвязь между цепными и базисными абсолютными приростами следующая: Сумма последовательных абсолютных цепных приростов равна базисному абсолютному приросту последнего уровня.

Интенсивность изменения уровней временного ряда характеризуется темпами роста и прироста.

Темп роста есть отношение двух уровней ряда. Они также могут рассчитываться как цепные и базисные:

,

.

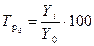Показатели роста, выраженные в коэффициентах, принято называть коэффициентами роста.

Цепные тепы роста характеризуют интенсивность изменения уровней от года к году, базисные темпы роста фиксируют интенсивность роста (снижения) за весь интервал времени между текущими и базисными уровнями.

Взаимосвязь между базисными и цепными коэффициентами роста следующая:

1) произведение цепных коэффициентов роста равно базисному коэффициенту роста последнего периода:

;

2) частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту роста:

.

Темп прироста характеризует абсолютный прирост в относительных величинах и показывает, на сколько процентов изменился сравниваемый уровень по отношению к базе сравнения.

,

,

.

Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1 % прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за тот же промежуток времени:

,

т.е. абсолютное значение 1 % прироста в данном периоде есть сотая часть достигнутого уровня в предыдущем периоде.

Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как

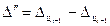
и показывает, на сколько данная скорость изменения уровней больше или меньше предыдущей.

Если систематически растут цепные темпы роста, то ряд развивается с относительным ускорением. Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста:

или

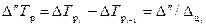
Полученная величина выражается в процентных пунктах (п.п.).

Коэффициент опережения определяется как отношение последующего темпа роста к предыдущему:

.

Его рассчитывают в сравнительном анализе нескольких рядов динамики, их приводят к одному основанию путем расчета базисных темпов роста с одинаковой по времени базой сравнения. Это позволяет наглядно видеть, для какого ряда интенсивность изменения уровней наибольшая. Сравнивая далее наибольшие темпы роста с наименьшими, определяют коэффициенты опережения в развитии одного явления по отношению к другому.

Для обобщения данных по рядам динамики рассчитываются:

· средний уровень ряда;

· средний абсолютный прирост;

· средние темпы роста и прироста.

Средний уровень ряда интервальных и моментных рядов определяется по-разному.

Для интервальных рядов динамики с равноотстоящими во времени уровнями расчет среднего уровня проводится по формуле простой средней арифметической:

,

где n – число уровней ряда.

Для интервальных временных рядов с не равноотстоящими во времени уровнями средний уровень рассчитывается по средней арифметической взвешенной:

,

где t_i – величина интервала между уровнями.

Для моментных рядов динамики с равноотстоящими во времени уровнями средний уровень (средняя хронологическая) находится по формуле:

.

В случае моментных временных рядов с не равноотстоящими во времени уровнями средний уровень определяется по формуле средней хронологической взвешенной:

,

где t_i – продолжительность интервала времени между соседними уровнями.

Кроме среднего уровня, при анализе и прогнозировании широко используются средние показатели изменения уровней ряда, а именно, средний абсолютный прирост и средний темп роста.

Средний абсолютный прирост показывает, на сколько в среднем увеличился или уменьшился уровень за изучаемый период:

.

Средний темп роста отражает интенсивность изменения уровней ряда. Он показывает, сколько в среднем процентов последующий уровень составляет от предыдущего на всем периоде наблюдения:

.

Соответственно средний темп прироста определяется на основе среднего темпа роста:

.

Пример 9.2 – Рассмотрим расчет показателей динамики (таблица 9.2). Наибольший абсолютный цепной прирост наблюдался в 2008 г., его величина, составила: 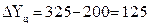шт. Наименьшее значение данного показателя в 2010 г.: шт.). В относительном выражении рост производства продукции составил: в 2008 г. по сравнению с 2007 г. - 162,5 % (), а в 2010 г. по сравнению с 2009 г. 124,14 % (). Следовательно, в 2008 г. производство продукции возросло на 125 шт. или на 62,5 %, а в 2010 г. – на 105 шт. или 24,14 % по сравнению с предыдущим годом. Базисные показатели динамики свидетельствуют о постоянном росте исследуемого показателя в анализируемом периоде: в 2011 г. произведено продукции на 450 шт. больше, чем в 2007 г. (базисном), что составило 225 %.

Проверим взаимосвязь между цепными и базисными показателями изменения уровней ряда:

а) сумма цепных абсолютных приростов равна базисному приросту (см. таблицу 9.2, где в итоговой строке накопленный прирост за 2008 – 2011 г.г. – 450 шт. – совпадает с базисным абсолютным приростом для 2011 г.);

б) произведение цепных коэффициентов роста равно базисному или равносильное этому деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентам роста. Так, по данным таблицы 9.2, имеем:

, или 325 % – базисный темп роста;

217,50/162,50= 1,3385, или 133,85 % – цепной коэффициент роста для 2009 г.

Взаимосвязь цепных и базисных темпов (коэффициентов) роста позволяет при анализе, если необходимо, переходить от цепных показателей к базисным, и наоборот.

Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1 % прироста (см. таблицу 9.2, последнюю графу).

Для обобщения данных по рядам динамики рассчитаем:

· средний уровень ряда;

· средний абсолютный прирост;

· средний темп роста и прироста.

Таблица 9.2 - Динамика объема продукции по предприятию

Год	Произведено продукции, шт.	Абсолютные приросты, шт.	Темпы роста, %	Темпы прирост, %	Абсолютное значение 1 % прироста, шт.
цепные	базисные	цепные	базисные	цепные	базисные
		-	-	-		-	-	-
				162,50	162,50	62,50	62,50	2,00
				133,85	2,18 раз	33,85	117,50	3,25
				124,14	2,70 раз	24,14	170,00	4,35
				120,37	3,25 раз	20,37	2,25 раз	5,40
Итого			-	-	-	-	-	-

По интервальному динамическому ряду из абсолютных величин с равными интервалами средний уровень определяется по средней арифметической простой из уровней ряда.

По данным таблицы 9.2, средний за период объем произведенной продукции составит:

у = 2150/5 = 430 шт.

Средний абсолютный прирост применительно к таблице 9.2 составит:

шт.

Средний темп роста и темп прироста соответственно равны:

, или 134,27 %;

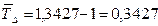, или 34,27 %

Следовательно, производство продукции в среднем за анализируемый период составило 430 шт. в год. Причем ежегодно оно возрастало в среднем на 113 шт. или на 34,27 %.

Дата добавления: 2014-01-04