Аналитическое сглаживание (выравнивание) рядов динамики

Аналитическое выравнивание динамических рядов - это нахождение определенной модели (уравнения тренда), которая математически описывает тенденцию развития явления во времени. При этом уровни показателя рассматриваются только

как функция от времени. В отличие от рассмотренных выше методов, таких, как укрупнение интервалов, скользящих средних, направленных в основном на то, чтобы ответить на вопрос: есть ли тенденция в динамическом ряду или нет, и определить ее направление, аналитическое выравнивание позволяет более точно установить характер развития явления, а главное - описать его математически, уловить все нюансы и направления развития и, что, пожалуй, наиболее интересно, использовать в дальнейшем полученную модель для прогнозирования.

Таблица 9.6 - Сглаживание ряда динамики методом скользящей средней по четырем членам

Исходные данные	Расчетные данные
Месяц	Поставки товаров, млн. р.	Нецентрированные скользящие средние по четырем членам, млн. р.	Центрированные скользящие средние по четырем членам, млн. р.,	Месяц
Январь		-	-	Январь
-
Февраль		-	Февраль
Март			Март
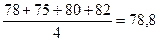
Апрель			Апрель
Май			Май
Июнь		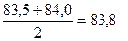	Июнь
Июль			Июль
Август			Август
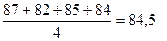
Сентябрь			Сентябрь
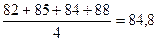
Октябрь			Октябрь
Ноябрь		-	Ноябрь
-
Декабрь		-	Декабрь
-

Первым шагом в проведении аналитического выравнивания является выбор вида математической функции, которую предполагается использовать в качестве модели тренда. При этом можно руководствоваться формой кривой, полученной на основе отображения на графике эмпирических данных. Схема построения графика достаточно проста: по оси абсцисс откладываются временные периоды (даты), по оси ординат - значения уровней динамического ряда.

При анализе рядов динамики в качестве линии тренда чаще всего используются следующие функции:

-линейная: = a ₀+ a ₁ t;

-парабола 2-го порядка: = a ₀+ a ₁ t + a ₂ t ²;

-показательная: = a ₀× a ₁ t ²

-гиперболическая: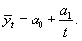

Кроме того, возможности современного программного обеспечения (например, ППП STATISTICA) позволяют использовать в качестве модели тренда математическую функцию любого (задаваемого пользователем) произвольного вида.

Выравнивание по линейной функции (прямой). Выбор в пользу выравнивания по линейной функции производят либо по результатам графического анализа эмпирических данных, либо если уровни ряда меняются в арифметической прогрессии (в этом случае рассчитанные цепные абсолютные приросты уровней приблизительно одинаковы).

При выравнивании по линейной функции (прямой) используется уравнение вида

= a ₀+ a ₁ t,

где t - условный показатель времени.

Параметры уравнения определяются на основе метода наименьших квадратов путем решения системы нормальных линейных уравнений

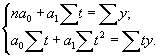
В качестве примера рассмотрим динамический ряд, представленный в таблице 9.7.

Таблица 9.7 - Доход банков от операций с ценными бумагами за 2005-2010 гг.

Год
Доход банков от операций с ценными бумагами, млн. р., y
Цепные абсолютные приросты	-

Итак, рассчитанные нами цепные абсолютные приросты относительно постоянны, поэтому можно говорить о целесообразности выбора в качестве аналитической функции уравнения прямой.

При нахождении параметров уравнения показатель времени удобно обозначить так, чтобы выполнялось следующее равенство: [Σ t = 0]. Для этого при нечетном количестве уровней ряда моменту (периоду) времени, находящемуся в центре ряда, придается значение t = 0, предыдущим - присваивают значения минус 1, минус 2, минус 3 и т. д., а последующим - значения 1, 2, 3 и т. д. (т. е. с шагом 1 от середины ряда в одну и другую сторону от центра).

Предположим, что мы рассматриваем динамический ряд, имеющий пять уровней (за период с 2006 по 2010 г.), тогда условный показатель времени обозначим так, как это показано в таблице 9.8.

Таблица 9.8 - Обозначение условного показателя времени при нечетном количестве уровней динамического ряда

Год
Доход банков от операций с ценными бумагами, млн. р., y
Условный показатель времени, t	-2	-1

При четном количестве уровней в середине ряда находятся два момента (периода) времени. Одному из них присваивают значение t = минус 1, а другому t = +1. Тогда предыдущие моменты времени получают значения минус 3, минус 5 и т. д., а последующие значения - +3, +5 и т. д. (т. е. с шагом 2 в одну и другую сторону от центра).

При подобном способе обозначения времени система уравнений упрощается

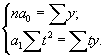
Тогда коэффициенты уравнения а ₀ и а ₁ находят следующим образом:

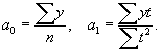
Определим по данным таблицы 9.9, в которой представлен ряд динамики с четным числом уровней, параметры уравнения прямой (таблица 9.9).

Таблица 9.9 - Расчетная таблица для определения параметров уравнения прямой

Год	Доход банков от операций с ценными бумагами, млн. р., y	t	t^2	y·t	Выравненные значения,
		-5		-350	68,43
		-3		-276	91,258
		-1		-112	114,09
					136,91
					159,74
					182,57
Сумма

Тогда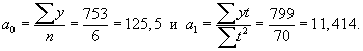

Искомое уравнение прямой имеет вид: = 125,5 + 11,414 t.

Подставляя в полученное уравнение соответствующее значение t, рассчитаем выравненные теоретические значения показателя (см. последнюю графу таблицы 9.9). При этом сумма выравненных значений должна равняться сумме эмпирических значений (753), если это не так, то параметры уравнения определены неверно.

График, построенный по выравненным значениям показателя, будет отражать тенденцию развития явления во времени (рисунок 9.1).

На основе полученного уравнения тренда можно строить прогнозные значения показателя для разных периодов времени путем подстановки в полученное уравнение значений временной компоненты. Например, для 2012 г. получим следующую ожидаемую величину дохода:

= 125,5 + 11,414 t = 125,5 + 11,414 × 7 = 205,398 млн. р.

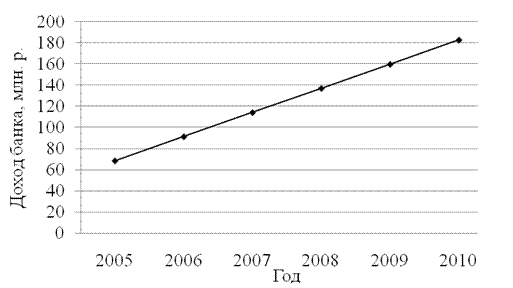
Рисунок 9.1 - Уравнение прямой, описывающее изменение во времени
дохода банков от операций с ценными бумагами

Выравнивание по параболе второго порядка. При ускоренном или замедленном изменении уровней динамического ряда, когда постоянны рассчитанные вторые разности уровней (цепные абсолютные приросты цепных абсолютных приростов), для аналитического выравнивания применяют параболу второго порядка:

= a ₀+ a ₁ t + a ₂ t ².

Параметры уравнения находят на основе метода наименьших квадратов, при этом обозначение условного показателя времени t абсолютно аналогично обозначению времени при построении прямой.

Система нормальных уравнений для нахождения параметров уравнения параболы имеет вид:

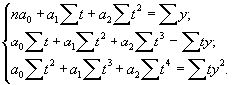
Если принять обозначение времени, при котором выполняется равенство S t = 0, рассматриваемую систему уравнений можно упростить. Она примет следующий вид:

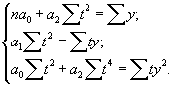
Проведем аналитическое выравнивание данных, характеризующих динамику инвестиций за период 2005-2010 гг. (таблица 9.10).

Таблица 9.10 - Динамика инвестиций за 2005-2010 гг.

Показатель	Год
Инвестиции, млн. р., Y
Первые разности (цепные абсолютные приросты),	-
Вторые разности,	-	-

Рассчитанные вторые разности демонстрируют относительное постоянство, поэтому в качестве аналитической функции для выравнивания возьмем уравнение параболы второго порядка. Наш выбор подтверждает и графический анализ данных (рисунок 9.2).

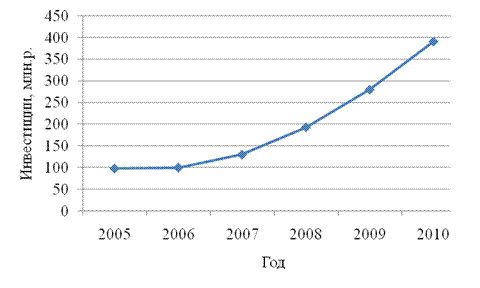
Рисунок 9.2 - Динамика инвестиций за 2001-2006 гг.

Проведем необходимые расчеты для определения параметров уравнения в таблице 9.11.

Таблица 9.11 - Расчетная таблица для определения параметров уравнения параболы второго порядка

Год	Инвестиции, млн. р., y	t	t^2	t^4	y·t	y·t^2	Выравненные значения,
		-5			-490
		-3			-300
		-1			-130
Сумма

Построим и решим систему уравнений (таблица 9.15):

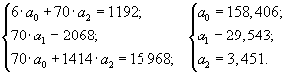
Таким образом, искомое уравнение параболы имеет вид

=158,406 + 29,543 t + 3,451 t ².

Выравнивание по показательной функции. Если уровни ряда меняются в геометрической прогрессии, т. е. рассчитанные цепные коэффициенты роста относительно постоянны, то для выравнивания используют показательную функцию вида

= a ₀×.

Параметры показательного уравнения определяются путем решения следующей системы нормальных уравнений:

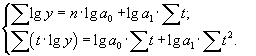
Если принять обозначении времени t, при котором выполняется условие Σ t = 0, система гораздо упрощается:

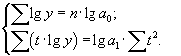
Проведем аналитическое выравнивание данных, характеризующих изменение числа страховых компаний региона за период 2005-2011 гг. (таблица 9.12).

Относительно постоянные цепные коэффициенты роста позволяют в качестве аналитического выражения тренда выбрать показательную функцию.

Таблица 9.12 - Динамика числа страховых компаний региона за 2005-2011 гг.

Год
Число страховых компаний, yi
Цепные коэффициенты роста	-	1,023	1,014	1,027	1,026	1,026	1,029

Проведем необходимые расчеты для определения параметров выбранного уравнения в таблице 9.13.

Таблица 9.13 - Расчетная таблица для определения параметров показательной функции

Год	Число страховых компаний, yi	t	t^2	lg y	t·lg y
		-3		2,3324	-6,997
		-2		2,3424	-4,685
		-1		2,3483	-2,348
				2,3598
				2,3711	2,3711
				2,382	4,764
				2,3945	7,1834
Итого				16,531	0,288

Составим и решим систему нормальных уравнений:

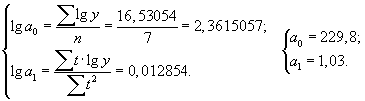
Показательное уравнение будет иметь вид

= 229,8 × 1,03 ^t

Подставляя в полученное уравнение значения условного показателя времени t, рассчитаем выравненные значения.

Выравнивание по гиперболе. Если уровни динамического ряда снижаются, постепенно замедляя свою скорость, но по логике никогда не смогут достичь нуля, то для проведения аналитического выравнивания выбирают уравнение гиперболы

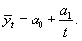
Параметры этого уравнения определяются на основе решения следующей системы нормальных уравнений:

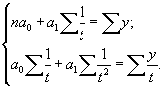
При нахождении параметров гиперболы применение принципа «отсчета от условного нуля», который использовался при нахождении параметров прямой, параболы и показательной функции, становится невозможным из-за выражения (1/t) при котором t = 0. Поэтому моменты (периоды) времени просто нумеруются, т. е. условному показателю времени присваиваются значения (1, 2, 3 и т. д.) начиная с первого уровня ряда.

Произведем аналитическое выравнивание данных, характеризующих изменение себестоимости единицы продукции вида «А» в течение года (таблица 9.14).

Таблица 9.14 - Расчетная таблица для нахождения параметров уравнения гиперболы

Месяц	Себестоимость единицы продукции вида "А", р. (y)	t	1/ t	t ^2	1/ t ^2	y / t
Январь			1,00000		1,0000	58,0000
Февраль			0,50000		0,2500	26,0000
Март			0,33333		0,1111	16,0000
Апрель			0,25000		0,0625	11,2500
Май			0,20000		0,0400	8,8000
Июнь			0,16667		0,0278	7,1667
Июль			0,14286		0,0204	6,1429
Август			0,12500		0,0156	5,2500
Сентябрь			0,11111		0,0123	4,6667
Октябрь			0,10000		0,0100	4,2000
Ноябрь			0,09091		0,0083	3,8182
Декабрь			0,08333		0,0069	3,4167
Сумма		-	3,10321	-	1,5650	154,7110

Составим систему уравнений

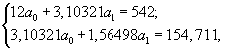
откуда находим значения параметров

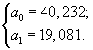
Уравнение гиперболы примет вид

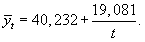
Подставив в полученное уравнение значения условного показателя времени t, рассчитаем выравненные значенияи поместим их в расчетную таблицу. Как видим, выравненные значения достаточно близки к эмпирическим данным, что позволяет надеяться на получение достоверных прогнозов на основе построенной модели.

При проведении аналитического выравнивания зачастую бывает трудно заранее определить подходящий вид уравнения тренда, особенно если эмпирические данные графически явно не демонстрируют относимость к какой-либо аналитической функции. Тогда поступают следующим образом: строят несколько уравнений тренда. Затем для каждого из них вычисляют остаточную дисперсию и модель с наименьшей величиной остаточной дисперсии признают лучшей из имеющихся на данный момент.

Остаточная дисперсия исчисляется по формуле

Это более простой метод, но есть и другие, более сложные методы.

Дата добавления: 2014-01-04