Процесса в линейной стационарной системе

Лекция 9. Спектральный метод расчета установившегося случайного

Этот приближенный аналитический метод, называемый также методом передаточных функций, основан на использовании структурно-динамических схем систем и спектральных плотностей случайных процессов. Непосредственное использование спектральных плотностей возможно только для стационарных процессов. Поэтому данный метод позволяет строить модели процессов, соответствующих некоторым установившимся режимам в стационарных системах при стационарных воздействиях.

Применение спектрального метода основано на использовании двух свойств линейных систем:

1. Реакция линейной системы на совокупность входных воздействий может быть определена как сумма ее реакций на каждое из них в отдельности (принцип суперпозиции).

2. Случайный сигнал на выходе физически реализуемого линейного динамического звена имеет закон распределения, близкий к нормальному (свойство фильтра).

Второе свойство, строго говоря, имеет место при следующем соотношении между порядком знаменателя n и числителя m передаточной функции звена или системы: n – m ≥ 2. Однако его обычно используют во всех случаях, когда выполняется условие физической реализуемости n–m ≥ 1.

Благодаря указанным свойствам оказывается возможным изолированно рассматривать преобразование линейной системой детерминированных и центрированных случайных составляющих входных сигналов и ограничиваться для выходного сигнала или ошибки системы нахождением только математического ожидания и дисперсии, полностью определяющих нормальный закон распределения. Для оценки корреляционных свойств выходных сигналов используются корреляционные функции и спектральные плотности.

Каждый случайный входной сигнал преобразуется в сумму, например, задающее воздействие (рис. 45):

,

где m_g (t) - детерминированная составляющая, или математическое ожидание входного сигнала; - центрированная случайная составляющая входного сигнала (случайный процесс с нулевым математическим ожиданием). Аналогичными суммами описываются возмущающие воздействия и выходные сигналы.

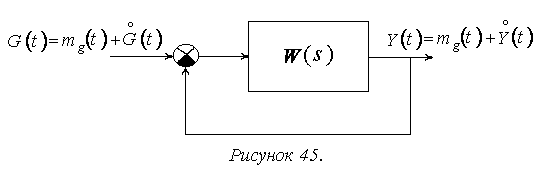
Модель преобразования детерминированной составляющей строится на основе стандартного аппарата передаточных функций (рис. 46):

L [ m_y (t)] = Φ(s) L [ m_g (t)],

L [ m_x (t)] = Φ _x (s) L [ m_g (t)],

где L [ m_g (t)], L [ m_y (t)], L [ m_y (t)] - изображения по Лапласу детерминированных составляющих соответственно входного сигнала g, выходного сигнала y и сигнала ошибки системы x; Φ(s) – основная передаточная функция системы, Φ _x (s) – передаточная функция по ошибке. Для системы на рис. 46

, .

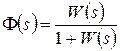Выходной сигнал в установившемся процессе может быть определен по теореме о конечном значении:

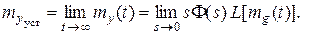(9.1)

Например, при m_g (t)= const для асимптотически устойчивой системы из (9.1) получим: m_y =Φ(0) m_g = const.

Аналогично для сигнала ошибки от задающего воздействия: 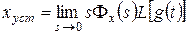, а также с использованием соответствующих передаточных функций для реакций системы на возмущающее воздействие.

Модель преобразования центрированной случайной составляющей (рис. 47) строится для спектральных плотностей

S_y (ω)=|Φ(j ω)|² S_g (ω), (9.2)

где спектральная плотность входного сигнала определяется по его корреляционной функции

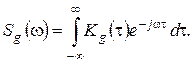
По полученной спектральной плотности выходного сигнала находят его дисперсию:

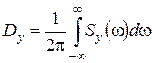. (9.3)

Интеграл вида (9.3) обычно удается привести к форме:

,

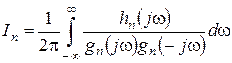где h_n (j ω)= b ₁(j ω)^{2 n -2} + b ₂(j ω)^{2 n -4} +... +b_n, g_n (j ω)= a ₀(j ω) ⁿ + a ₁(j ω) ^{n -1} +... +a_n.

Тогда:

,

где ∆_n - n -й определитель Гурвица для многочлена g_n (s), а ∆'_n получается из ∆_n заменой первой строки коэффициентами многочлена h_n. Например, при n =4:

, .

Для системы с несколькими случайными входными сигналами ограничимся случаем, когда они не коррелированы между собой.

Пусть в системе присутствуют случайные задающее G (t) и несколько возмущающих воздействий F_k (t), k= 1,2,…, K, приложенные в различных точках (рис. 48).

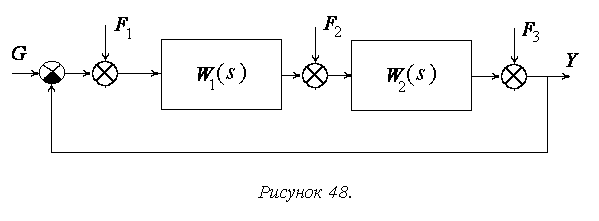
Тогда каждый сигнал раскладывается в сумму детерминированной и случайной составляющих , , k= 1,2,…, K. После этого математическое ожидание и дисперсия выходного сигнала определяются на основе принципа суперпозиции:

,

, (9.4)

где и - математическое ожидание и спектральная плотность k -го возмущающего воздействия; - передаточная функция системы по k -му возмущающему воздействию.

Таким образом, выходной сигнал определяется в форме , причем центрированная случайная составляющая описывается дисперсией D_y.

Аналогичный подход используется при нахождении ошибки системы. Она определяется в форме: .

Математическое ожидание ошибки определяется в виде суммы:

,

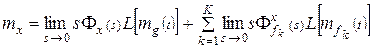где - передаточная функция системы по ошибке от k -го возмущающего воздействия.

При детерминированном задающем воздействии (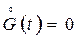) дисперсия ошибки совпадает с дисперсией выходного сигнала, определяемой в соответствии с (9.4).

Дата добавления: 2014-01-04