Этапы построения гистограммы

Гистограмма

Советы по использованию диаграмм

1. Установите важность каждой причины на основе объективных значений или данных.

Анализ факторов с помощью собственного опыта или знаний возможен, но устанавливать их важность только на основе субъективных представле­ний или впечатлений опасно. Объективное установление важности факто­ров с помощью данных — более научный и логический подход.

3.Пытайтесь постоянно совершенствовать причинно-следственную диаграмму.

Гистограмма - это инструмент, позволяющий зрительно оценить закон распределения величины разброса данных, а также принять решение о том, на чем следует сфокусировать внимание для целей улучшения процесса.

Гистограмма отображается серией столбиков одинаковой ширины, но разной высоты. Ширина столбика представляет интервал в диапазоне наблюдений, высота — количество наблюдений (измерений), попавших в данный интервал. При нормальном законе распределения данных существует тенденция расположения большинства результатов наблюдений ближе к центру распределения (к центральному значению) с постепенным уменьшением при удалении от центра.

Гистограмма применяется главным образом для анализа значений измеренных параметров, но может использоваться и для оценки показателей возможностей процессов.

Систематизируя показатели качества и анализируя построенную для них гистограмму, можно легко понять вид распределения, а определив среднее значение показателя и стандартное отклонение, можно провести сравнение показателей качества с контрольными нормативами и таким образом получить информацию высокой точности.

Рассмотрим порядок построения гистограммы, характеризующей управляемость процесса производства валиков, с использованием данных приведенного ниже контрольного листка.

Построение гистограммы, как правило, включает в себя следующие этапы

1. Разработка формы контрольного листка для сбора первичных данных (см.1). Пример такого контрольного листка для процесса производства валиков приведен ниже.

2. Сбор статистических данных xi, i = 1, 2,..., N, характеризующих ход процесса, и заполнение второго столбца контрольного листка. После заполнения контрольного листка приступают собственно к построению гистограммы. 3. Вычисление диапазона данных (выборочного размаха) где x max — наибольшее наблюдаемое значение; x min — наименьшее наблюдаемое значение.

4. Определение количества интервалов п на гистограмме часто осуществляют по формуле Стерджесса

. 5. Определение размеров интервалов осуществляют так, чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины. Для получения ширины интервалов h = R/n размах R делят на полученное выше количество интервалов п.

Желательно, чтобы размер интервала был не менее двух делений шкалы измерительного прибора.

6. Определение границ интервалов.

Сначала определяют нижнюю границу первого интервала и прибавляют к ней ширину этого интервала, чтобы получить границу между первым и вторым интервалами. Далее продолжают прибавлять найденную ширинуинтервала h к предыдущему значению для получения второй границы, затем третьей и т. д. После завершения такой работы можно удостовериться, что верхняя граница последнего интервала совпадает с максимальным значением х mах.

7. Вычисление частот.

В третий столбец таблицы контрольного листка вносят количество значений, попавших в каждый интервал. По результатам наблюдений, отмеченных черточками во втором столбце этой таблицы, подсчитывают общее количество наблюдений (в нашем случае N = 88), а затем в четвертый столбец записывают относительные частоты, выраженные в процентах

8. Построение горизонтальной и вертикальной осей графика.

Берется миллиметровая бумага, на ней наносятся горизонтальная и вертикальная оси, а затем на каждой оси выбираются масштабы.

9. Построение графика гистограммы.

На горизонтальную ось необходимо нанести границы интервалов. На оси абсцисс с обеих сторон (перед первым и после последнего интервалов) следует оставить место, не менее размера одного интервала. Пользуясь шириной интервалов как основанием, строят прямоугольники, высота каждого из которых равна частоте попадания результатов наблюдений в соответствующий интервал. На график (см. рис. 3.2) наносят линию, представляющую среднее арифметическое значение , а также линии, представляющие границы поля допуска, если они имеются. 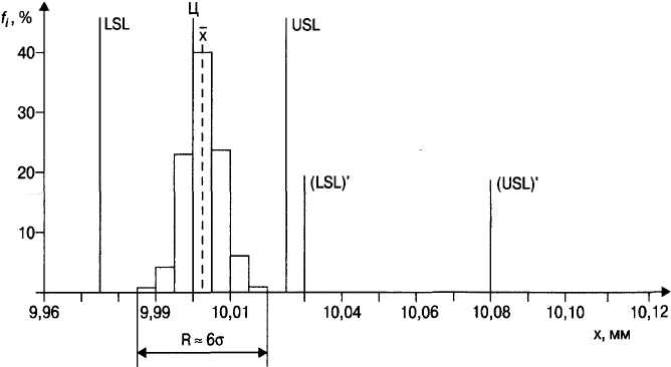. Типовые формы гистограмм

На рис. 3 приведены наиболее часто встречающиеся на практике формы (типы) гистограмм

Полезную информацию о характере распределения случайной величины можно получить, взглянув на форму гистограммы. Формы, представленные на рис. 3.3, типичны, и вы можете воспользоваться ими как образцами при анализе процессов.

Рис..3. Основные формы гистограмм:

а — симметричная, или колоколообразная;

в — положительно скошенное распределение;

д — равномерное распределение (плато);

б — гребенка;

г — распределение с обрывом справа;

е — двухпиковая (бимодальная) форма

Обычная форма (симметричная, или колоколообразная). Среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается к обоим концам. Форма симметрична.

Примечание. Это именно та форма, которая встречается чаще всего.

Гребенка Интервалы через один имеют более низкие (высокие) частоты.

Примечание. Такая форма встречается, когда число единичных наблюдений, попадающих в интервал, колеблется от интервала к интервалу или когда действует определенное правило округления данных.

Положительно скошенное распределение (отрицательно скошенное распределение). Среднее значение гистограммы локализуется слева (справа) от центра размаха.

Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно — при движении вправо (влево). Форма асимметрична.

Примечание. Такая форма встречается, когда левое (правое) значение поля допуска недостижимо.

Распределение с обрывом справа (распределение с обрывом слева). Средне арифметическое гистограммы локализуется далеко слева (справа) от центра разма-ха. Частоты резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма асимметрична.

Примечание. Это одна из тех форм, которые часто встречаются при 100 %-ной разбраковке изделий из-за плохой управляемости процесса, а также когда проявляется резко выраженная положительная (отрицательная) асимметрия.

Равномерное или прямоугольное распределение (плато). Частоты в разных интервалах образуют плато, поскольку все интервалы имеют более или менее одинаковые ожидаемые частоты.

Примечание. Такая форма встречается в смеси нескольких распределений, имеющих различные средние значения.

Двухпиковая (бимодальная) форма. В окрестностях центра диапазона данных частота низкая, т. е. по пику с каждой стороны.

Примечание. Такая форма встречается, когда смешиваются два распределения с далеко отстоящими центрами.

Дата добавления: 2014-01-04