Факторгруппа

ЛЕКЦИЯ 11

Значение нормального делителя в теории групп основано на том, что из смежных классов по нормальному делителю может быть построена новая группа. Для построения такой группы определим операцию умножения на множестве смежных классов. Пусть 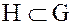, тогда

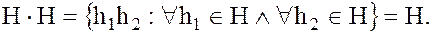(1)

Действительно, для

Пусть H – нормальный делитель группы G.

В этом случае произведение двух смежных классов G по H будет смежным классом по H. Действительно, имеем:

(2)

Таким образом, на множестве всех левых смежных классов по нормальному делителю определена операция умножения. Это означает, что фактормножество

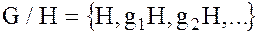. (3)

является замкнутым относительно операции умножения смежных классов, а операция умножения смежных классов является алгебраической.

Равенство (2) показывает, что для нахождения произведения двух данных смежных классов группы G по нормальному делителю H надо в каждом из этих классов выбрать по одному представителю и потом взять тот смежный класс, к которому принадлежит произведение выбранных представителей.

В случае если 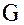– абелева группа, бинарная операция на фактормножестве вводится соотношением

.

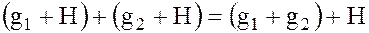Теорема. Фактормножество 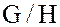смежных классов группы G по нормальному делителю H с определенной в нем операцией умножения является группой.

Эта группа называется факторгруппой группы G по нормальному делителю H и обозначается символом .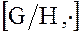

Доказательство. Для доказательства покажем, что в будут выполнены все аксиомы группы:

· ассоциативность умножения смежных классов следует из ассоциативности умножения подмножеств группы;

· роль единицы играет сама подгруппа – нормальный делитель:

· для смежного класса обратным является класс действительно:

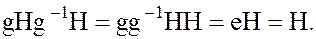
Замечание. Факторгруппу 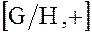часто называют группой 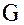по модулю .

Выводы. Со всякой группой G связан целый набор новых групп – ее факторгрупп [G/H, ×] по различным нормальным делителям.

Пример. 1. Пусть 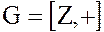– аддитивная группа целых чисел, а 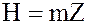– подгруппа целых чисел, делящихся на m без остатка. Подгруппа 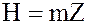– нормальный делитель так как – подгруппа аддитивной группы.

Факторгруппа 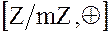состоит из смежных классов – классов вычетов по модулю :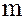

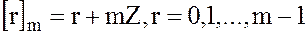
Каждым двум классам 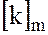и 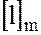, независимо от выбора в них представителей , , 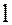можно поставить в соответствие классы, являющиеся их суммой или произведением, т.е. на множестве классов вычетов по модулю 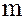однозначным образом индуцируются операции сложения и умножения по модулю :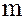

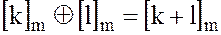
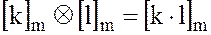
Пусть , тогда таблица Кэли для факторгруппы имеет вид:

	[0]5	[1]5	[2]5	[3]5	[4]5
[0]5	[0]5	[1]5	[2]5	[3]5	[4]5
[1]5	[1]5	[2]5	[3]5	[4]5	[0]5
[2]5	[2]5	[3]5	[4]5	[0]5	[1]5
[3]5	[3]5	[4]5	[0]5	[1]5	[2]5
[4]5	[4]5	[0]5	[1]5	[2]5	[3]5

Выводы:

1. Факторгруппа коммутативна – таблица Кэли симметрична относительно главной диагонали.

2. Факторгруппа циклическая группа 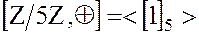. Порядок этой группы равен 5. Одним из бразующих элементов этой группы является смежный класс 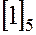, а все остальные смежные классы совпадают с его степенями. Так как порядок группы равен 5, а 5-простое число, то в соответствии с обращением теоремы Лагранжа она не имеет собственных подгрупп.

Замечание.

1.Так как операции на смежных классах сводятся к соответствующим операциям над числами из классов вычетов, то для фиксированного 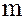индекс 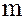можно опускать и вместо 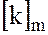использовать символ 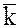. В этом случае операции сложения и умножения классов вычетов по модулю 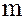принимают вид

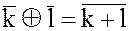
3. Высшим этапом освоения работы с классами вычетов по модулю 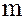является отказ от черточек и кружочков в записи классов вычетов и операций сложения и умножения . В этом случае оперируют с каким-либо фиксированным множеством представителей классов вычетов по модулю 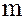, чаще всего - с множеством

4.

.

Это множество называется приведенной системой вычетов по модулю .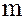

В этом случае операции сложения и умножения классов вычетов по модулю 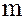принимают вид:

Пример 2. Пусть , тогда таблица Кэли для факторгруппы 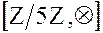имеет вид:

·

Замечание.

Как следует из таблицы Кэли, множество 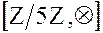не является группой, так как 0 не имеет обратного элемента. Если исключить 0 из множества 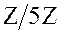, тогда множество с операцией умножения по модулю 5 будет группой, таблица Кэли для которой имеет вид:

·

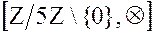
Порядок группы 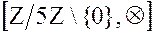равен 4. Группа циклическая с образующими элементами 2 или 3 т. е.

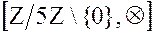=<2>=<3>.

В соответствии с обращением теоремы Лагранжа делителями числа 4 являются 1, 2 и 4. Это означает, что данная группа имеет собственную подгруппу H второго порядка. Элементами этой подгруппы будут классы вычетов {1,4}, т.е.

.

Таблица Кэли для этой подгруппы имеет вид:

·

Пример 3. Пусть . Построим таблицы Кэли для факторгрупп 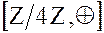и .

+

·

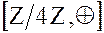
Замечания.

1. Факторгруппа 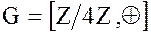является циклической группой с образующими элементами 1 или 3 и имеет порядок равный 4, т.е. .

В соответствии с обращением теоремы Лагранжа делителями числа 4 являются 1, 2 и 4. Это означает, что данная группа имеет собственную подгруппу H второго порядка. Элементами этой подгруппы будут классы вычетов {0,2}, т.е. .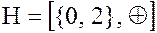

Таблица Кэли для этой подгруппы имеет вид:

+

3. Множество также не является группой, так как 0 не имеет обратного элемента. Исключая 0 из множества 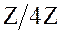, получаем множество 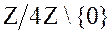классов вычетов по модулю 4 без 0, таблица Кэли для которого имеет вид:

·

Анализ таблицы Кэли показывает, что и в этом случае множество 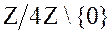классов вычетов по модулю 4 без 0 группой не является т. к. содержит 0 и, следовательно, множество 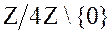классов вычетов по модулю 4 без 0 не замкнуто относительно операции умножения по модулю 4.

Дата добавления: 2014-01-04