Оценка дифференциального эффекта уровней фактора

Дифференциальный эффект уровней позволяет оценить изменение среднего значения отклика системы при переходе фактора с уровня j на уровень i. При этом следует учитывать, что на это изменение оказывает воздействие и случайные причины, а не только анализируемый фактор. Как и в дисперсионном анализе, здесь возможны различные варианты решения задачи в зависимости от наличия априорной информации и повторных опытов в точках плана. Рассмотрим два типовых варианта обработки данных.

В первом варианте рассматривается следующая ситуация:

- результаты измерений в различных точках независимы, повторные опыты отсутствуют;

- предполагается нормальное распределение значений функции отклика в различных точках плана, дисперсии распределения неизвестны, но одинаковы (случайность значений обусловлена ошибками измерений).

Данный вариант соответствует сравнению двух средних нормально распределенных генеральных совокупностей, дисперсии которых неизвестны, но предположительно одинаковы. Сравнение предполагает выполнение следующих шагов.

1. Вычисление средних значений функции отклика для двух сравниваемых значений факторов (уровни факторов соответствуют столбцам j и i латинского квадрата)

.

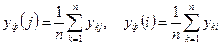2. Вычисление оценок дисперсии функции отклика для выбранных уровней факторов

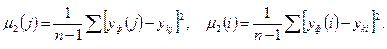
3. Прежде сравнения средних следует проверить однородность оценок дисперсии по критерию Фишера. Дисперсии расставляются так, чтобы значение критерия было больше единицы, например при D _ф(j) > D _ф(i) критерий F = D _ф(j)/ D ф(i). Если однородность нарушена, то проводить сравнение средних значений неправомочно, следует устранить выявленное нарушение или отказаться отданного варианта проверки.

4. Если неоднородность дисперсий не обнаружена, то можно установить значимо или незначимо различаются средние значения функции отклика для двух значений факторов, используя критерий Стьюдента. Гипотеза Н₀ соответствует утверждению y _ф(j) = y _ф(i). В качестве критерия проверки нулевой гипотезы выступает положительное значение случайной величины

Т = { [ y _ф(j) - y _ф(i)]/[ D _ф(j) + D _ф(i)]^0,5} { п(п — 1)}.

Эта величина при справедливости гипотезы Н ₀ имеет распределение Стьюдента с 2n - 2 степенями свободы. Критическая область зависит от вида альтернативной гипотезы Н₁.

Если Н₁ соответствует y _ф(j) ¹ y_ф(i), то критическая область является двусторонней. Критическое значение t _кр находится стандартным образом по заданной величине уровня значимости а и количеству степеней свободы. При Т>t _кр нулевая гипотеза отвергается, следовательно фактор оказывает существенное влияние на функцию отклика.

Если Н ₁ соответствует y _ф(j) > y _ф(i) или y _ф(i) > y _ф(j) то критическая область будет правосторонней. В остальном проверка аналогична предыдущему случаю.

Во втором варианте рассматривается следующая ситуация:

- в точках плана проведены повторные опыты. Пусть m – количество всех опытов при значении фактора Р_j, n – при значении факторов Р_i. Причём m > 30 и n > 30;

- результаты измерений в различных точках независимы.

В этом случае выборочные средние функции отклика распределены приближенно нормально, а оценки дисперсии являются достаточно хорошими приближениями к генеральным дисперсиям.

Порядок проверки гипотезы о значимости влияния фактора на уровнях j и i следующий.

Вычисляются средние значения функции отклика y _ф(j) и y _ф(i) по всем опытам при значениях фактора Р_j и Р_i. Затем рассчитываются дисперсии функции отклика D _ф(j) и D _ф(i) для двух значений фактора. дисперсия среднего значения случайной величины в т раз меньше дисперсии этой величины (здесь т - количество опытов).

В качестве гипотезы Н₀ выступает равенство y _ф(j) = y _ф(i). Поэтому в качестве критерия можно взять величину

и = | y _ф(j) - y _ф(i)|/{ D _ф(j)/ m + D _ф(j)/ q }^0,5,

которая в случае справедливости нулевой гипотезы распределена приближенно нормально с нулевым математическим ожиданием и единичной дисперсией (величина и является центрированной и нормированной). Проверка гипотез осуществляется аналогично случаям, рассмотренным выше, только вместо распределения Стьюдента применяется распределение стандартизованной нормальной величины.

Дата добавления: 2014-01-04