
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
При построении интервального вариационного ряда
|
|
|
|
Алгоритм группировки выборочных данных
1. Найти наименьшее и наибольшее значения признака в совокупности и определить размах варьирования
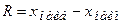 .
.
2. Определить число интервалов 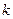 . Для этого можно использовать формулу Стерджесса:
. Для этого можно использовать формулу Стерджесса: 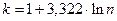 . Кроме того, в общей теории статистики принято ограничение:
. Кроме того, в общей теории статистики принято ограничение: 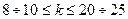 .
.
3. Найти постоянную величину (шаг) интервала 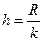 . Если окажется, что
. Если окажется, что 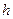 – дробное число, то в отдельных случаях, для обеспечения равной величины интервалов, его значение можно округлить в большую сторону.
– дробное число, то в отдельных случаях, для обеспечения равной величины интервалов, его значение можно округлить в большую сторону.
4. Определить границы интервалов. Если округление значения 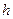 не проводилось, то за начало первого интервала следует взять
не проводилось, то за начало первого интервала следует взять 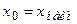 . Если же предварительно было выполнено округление, то в зависимости от разрядности округления, может быть выполнено смещение конца первого интервала влево. Промежуточные интервалы получаются прибавлением к концу предыдущего интервала длины частичного интервала
. Если же предварительно было выполнено округление, то в зависимости от разрядности округления, может быть выполнено смещение конца первого интервала влево. Промежуточные интервалы получаются прибавлением к концу предыдущего интервала длины частичного интервала 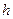 . Конец последнего интервала должен удовлетворять условию
. Конец последнего интервала должен удовлетворять условию 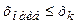 .
.
5. Подсчитать число выборочных данных, которые попадут в каждый из полученных интервалов:  ,
, 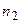 ,...,
,..., 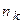 . При этом только один из промежутков будет замкнут с двух сторон
. При этом только один из промежутков будет замкнут с двух сторон 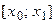 , а остальные промежутки будут замкнуты только справа:
, а остальные промежутки будут замкнуты только справа: 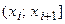 ,
, 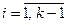 .
.
6. Результаты вычислений занести в таблицу, которая называется «Частотное распределение интервального вариационного ряда».
Пример 13.4. Данные (млн.ден.ед.) о дневной выручке частного бизнеса по результатам выборочного обследования торговых роллетов рынка приведены в таблице 13.1.
Построить интервальный вариационный ряд из 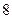 интервалов равной длины.
интервалов равной длины.
Решение. Наименьшее значение варианты в совокупности составляет 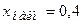 (млн.руб.), наибольшее −
(млн.руб.), наибольшее − 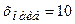 (млн.руб.), поэтому размах варьирования
(млн.руб.), поэтому размах варьирования 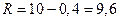 (млн.руб.).
(млн.руб.).
Так как по условию число интервалов  , то длина каждого интервала составит
, то длина каждого интервала составит  (млн.руб.).
(млн.руб.).
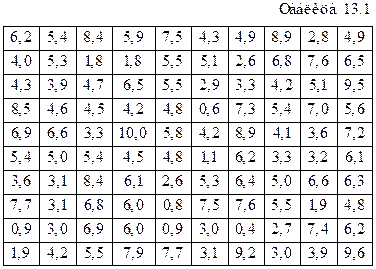
Выполнять округление в данном случае нет необходимости, поэтому за начало первого интервала примем 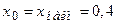 . Тогда по формуле
. Тогда по формуле  (
(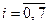 ), получим
), получим
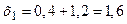 , ,
| 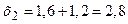 , ,
| 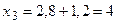 , ,
|
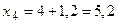 , ,
| 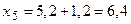 , ,
| 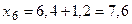 , ,
|
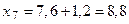 , ,
| 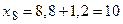 . .
|
Будем рассматривать следующие промежутки: 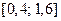 ,
, 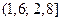 ,
, 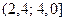 ,
, 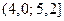 ,
, 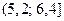 ,
, 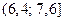 ,
,  ,
, 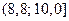 .
.
Найдем количество вариантов для каждого промежутка и результаты занесем в итоговую таблицу 13.2.
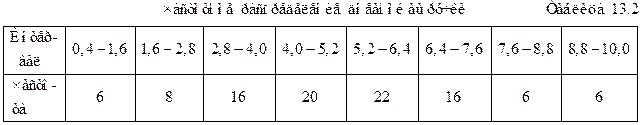
Для графического изображения вариационных рядов используют полигон частот и гистограмму.
Полигон служит для изображения дискретного вариационного ряда, представляет собой ломаную в прямоугольной системе координат, у которой концы отрезков прямой имеют координаты 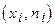 ,
, 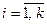 . Иногда при построении полигона добавляют фиктивные точки
. Иногда при построении полигона добавляют фиктивные точки 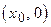 и
и 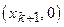 .
.
Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака в интервальном прямоугольном ряде, и высотами, равными частотам 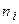 (частостям
(частостям 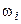 )
) 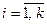 интервалов, в прямоугольной системе координат. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
интервалов, в прямоугольной системе координат. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
По виду полигона или гистограммы можно сделать предположение о законе распределения совокупности (признака).
Пример 13.3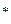 (продолжение). Построить полигон для полученного дискретного вариационного ряда.
(продолжение). Построить полигон для полученного дискретного вариационного ряда.
Ответ. Полигон представлен на рисунке 13.2.
Пример 13.4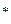 (продолжение). Построить гистограмму и полигон для полученного интервального вариационного ряда.
(продолжение). Построить гистограмму и полигон для полученного интервального вариационного ряда.
Ответ. Гистограмма и полигон представлены на рисунке 13.3.
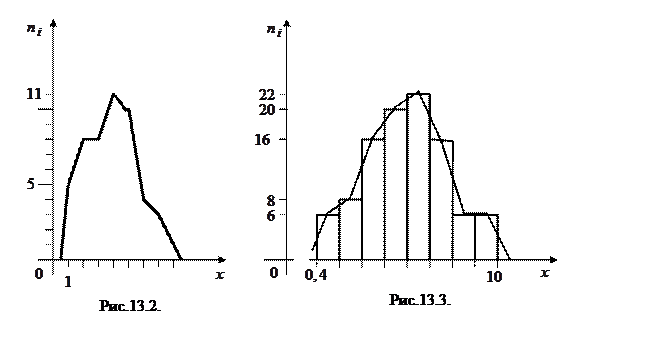
Определение 13.5. Эмпирической функцией распределения (функцией распределения выборки) называется функция  , определяющая для каждого значения
, определяющая для каждого значения 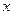 относительную частоту события
относительную частоту события 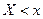 :
:
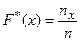 , (13.1)
, (13.1)
где 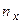 − число вариантов, меньших
− число вариантов, меньших 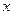 ,
, 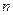 − объем выборки.
− объем выборки.
Свойства 
1. 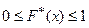 .
.
2.  − неубывающая функция.
− неубывающая функция.
3. 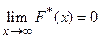 ,
, 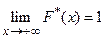 .
.
Если для некоторой совокупности 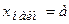 ,
, 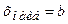 , то
, то 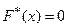 при
при 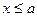 , и
, и 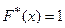 при
при  .
.
В случае построения эмпирической функции распределения для интервального вариационного ряда при ее графическом изображении можно соединить точки графика, соответствующие правым концам интервалов, отрезками прямой. В результате получим непрерывную линию, называемую кумулятивной кривой или кумулятой.
Пример 13.3 (продолжение). Для полученного дискретного вариационного ряда записать эмпирическую функцию распределения и построить ее график.
(продолжение). Для полученного дискретного вариационного ряда записать эмпирическую функцию распределения и построить ее график.
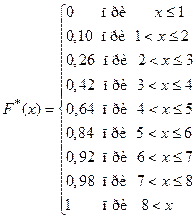 .
.
Ответ. График представлен на рисунке 13.4.
Пример 13.4 (продолжение). Для полученного интервального вариационного ряда записать эмпирическую функцию распределения и построить ее график, построить кумуляту.
(продолжение). Для полученного интервального вариационного ряда записать эмпирическую функцию распределения и построить ее график, построить кумуляту.
Ответ. Эмпирическая функция распределения имеет вид
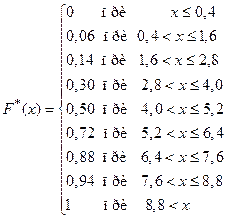
ее график и кумулята представлены на рисунке 13.5.
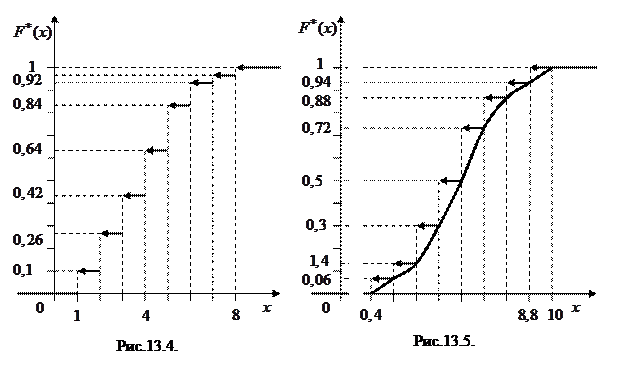
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 4386; Нарушение авторских прав?; Мы поможем в написании вашей работы!