Доказательство. При сферическом движении в твердом теле можно указать прямую, все точки которой будут иметь мгновенную скорость

Теорема 1

При сферическом движении в твердом теле можно указать прямую, все точки которой будут иметь мгновенную скорость, равную нулю.

По формуле Эйлера любая точка 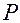тела при вращении вокруг неподвижной точки 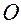имеет скорость

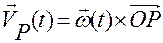, (3.13.1)

где 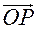— это положение точки 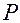относительно точки отсчета 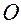в момент времени .

Оно может задаваться как вектором 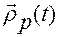с координатами 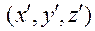в связанной системе, и тогда эти координаты будут постоянны, так и вектором 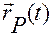с координатами 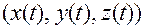в абсолютной системе, и тогда эти координаты будут функциями времени, причем

,

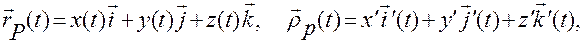
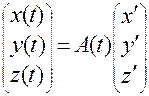где 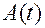— матрица ориентации.

Положим в (3.13.1) 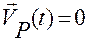(в фиксированный момент времени ). В таком случае из (3.13.1) вытекает

(3.13.2)

для любого .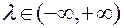

Если рассматривать соотношение (3.13.2) в абсолютном пространстве, то следует положить в нем . Вектор 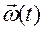следует считать заданным своими координатами в абсолютной системе.

При фиксированном значении времени и произвольных значениях 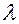соотношение (3.13.2) задает в абсолютном пространстве параметрическое уравнение прямой, проходящей через неподвижную точку .

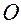Каждая такая прямая является геометрическим местом тех положений в абсолютном пространстве точек 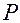твердого тела, в которых они (точки 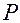) имеют скорость, равную нулю в момент времени .

Если рассматривать равенство (3.13.2) применительно к векторам 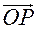, задаваемым в подвижном пространстве (в системе 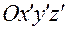, связанной с твердым телом), то в (3.13.2) следует положить 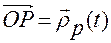. Тогда и вектор угловой скорости 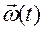должен рассматриваться в проекциях на связанные оси.

В таком случае при фиксированном значении времени
соотношение(3.13.2)

(3.13.2)

является параметрическим уравнением прямой в связанной системе.

Оно задает положения в теле всех тех его точек 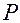, которые в момент имеют скорость, равную нулю. Теорема доказана.

Дата добавления: 2014-01-04