Подвижный аксоид и его уравнения

Запишем уравнение (3.13.2) в виде

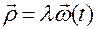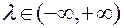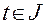, , . (3.13.3)

Пусть в правой части (3.13.3) вектор 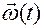задается своими проекциями 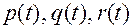на подвижные оси :

.

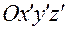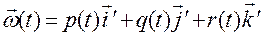Тогда вектор 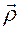, стоящий в левой части (3.13.3), определяется координатами 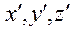в тех же подвижных осях:

.

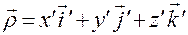Будем смотреть на величины 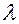и как на обобщенные координаты геометрической точки 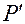, имеющей положение 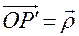в системе 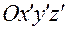. При таком рассмотрении правую часть (3.13.3) можно трактовать как вектор-функцию 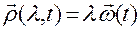, задающую связь обобщенных координат 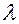, точки 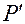с ее декартовыми координатами 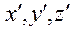в подвижной системе .

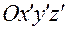В координатной форме эта связь записывается в виде:

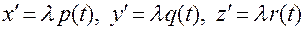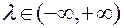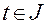, , . (3.13.4)

Система координат 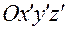является связанной системой для твердого тела, совершающего сферическое движение. Уравнение (3.13.3), рассматриваемое при фиксированном значении времени , задает в ней положения всех таких точек 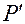, которые в этот момент находятся на мгновенной оси вращения твердого тела.

Если рассматривать уравнение (3.13.3) при всех значениях 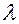и из области их изменения, то легко заметить, что оно определяет в системе 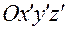годограф вектор-функции .

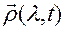Годограф образует в подвижном пространстве поверхность, которая состоит из точек пространства .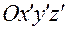

Каждая точка ее хотя бы в один момент времени принадлежит мгновенной оси вращения твердого тела.

Уравнения (3.13.4) являются параметрическими уравнениями указанной поверхности. Эту поверхность можно трактовать как абсолютно твердое тело, для которого 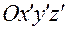служит связанной системой координат.

Дата добавления: 2014-01-04