Пример 14.1

Рассмотрим акцию с первоначальной ценой, равной 40 долл., ожидаемой доходностью, равной 16% годовых, и волатильностью, равной 20% годовых. Из равенства (14.3) следует, что распределение цены акции S_T через шесть месяцев будет иметь следующий вид:

ln S_T ~ ø[ln40 + (0,16 – 0,2²/2) × 0,5,02 ],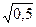

ln S_T ~ ø(3,759, 0,141).

Вероятность того, что нормально распределенная случайная величина лежит в окрестности математического ожидания на расстоянии, не превышающем 1,96 стандартных отклонений, равна 95%. Следовательно, с доверительной вероятностью, равной 95%, выполняется неравенство:

3,759 – 1,96 × 0,141 < lnS_T < 3,759 + 1,96 × 0,141.

Следовательно:

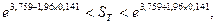
т.е.

32,55 < S_T < 56,56.

Итак, с 95%-ной верятностью цена акции через шесть месяцев будет лежать в диапазоне от 32,55 до 56,56 долл.

Переменная, имеющая логонормальное распределение, принимает значения от нуля до бесконечности. Форма этого распределения показана на рис. 14.1. В отличие от нормального распределения, логнормальное распределение является ассиметричным, поэтому его математическое ожидание, медиана и мода не совпадают друг с другом.

Из равенства (14.3) и свойств логнормального распределения следует, что математическое ожидание цены акции E(S_T) равно:

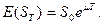(14.4)

Это полностью соответствует определению ожидаемой доходности µ. Можно показать, что дисперсия цены акции определяется по формуле:

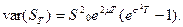(14.5)

Дата добавления: 2014-01-04