Волатильность

Пример из деловой практики 14.1. Доходность взаимных фондов может вводить в заблуждение.

Разница между параметрами µ и µ - σ²/2 часто появляется в отчетах о доходности взаимных фондов. Предположим, что управляющий некого взаимного фонда указал в отчете за пять лет следующие значения, представляющие собой показатели головой доходности:

15% 20% 30% - 20% 25%

Среднее арифметическое этих чисел, представляющее собой их сумму, деленную на пять, равно 14%. Однако инвестор, вложивший деньги на пять лет, на самом деле получит 14% годовых. Стоимость 100 долл. через пять лет будет равной следующей величине:

100 × 1,15 × 1,20 × 1,30 × 0,80 × 1,25 = 179,40 долл.

В противоположность этому, 14% годовых при ежегодном начислении принесло бы:

100 × 1,14⁵ = 192,54 долл.

Фактическая средняя доходность к концу пятого года равна:

100 × 1,124⁵ = 179,40 долл.

то есть 12,4% годовых.

Какую же среднюю доходность должен был указать управляющий взаимными фондами? Ему было бы выгодно заявить: «Средняя доходность, полученная нами за пять лет, равна 14%». Несмотря на то, что это правда, такое утверждение является неоднозначным. Намного точнее сказать «Средняя доходность, полученная вкладчиками нашего фонда за последние пять лет, равна 12,4% в год». В некоторых странах регулирующие органы требуют, чтобы управляющие инвестиционными фондами отчитывались именно так.

Это явление хорошо известно математикам. Так, среднее геометрическое нескольких чисел, не совпадающих друг с другом, всегда меньше среднего арифметического. В нашем примере доходность вычисляется путем последовательного умножения чисел 1,15, 1,20, 1,30, 0,80 и 1,25. Среднее арифметическое равно 1,140, а среднее геометрическое – только 1,124.

Волатильность цены акции σ представляет собой меру неопределенности ее доходности. Как правило, волатильность колеблется от 15% до 60%.

Из равенства (14.7) следует, что волатильность цены акции можно определить из как стандартное отклонение доходности акции за один год, когда доходность рассчитывается непрерывно.

Если величина Т невелика, из равенства (14.1) следует, что число 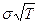приближенно равно стандартному отклонению относительно изменения цены акции за время Т. Допустим, что σ = 0,3, т.е. 30% годовых, а текущая цена акции равна 50 долл. Стандартное отклонение относительного изменения цены акции за одну неделю приближенно равно:

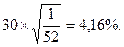
Следовательно, изменение цены акции за неделю равно 50×0,00416 = 2,08 долл.

Равенство (14.1) означает, что неопределенность будущей цены акции, измеренная с помощью стандартного отклонения, возрастает как корень квадратный из длины прогнозируемого интервала. Например, стандартное отклонение цены акции за четыре недели приближенно равно двум стандартным отклонениям цены за одну неделю.

Дата добавления: 2014-01-04