Лекция

Патология

· Неврит – воспаление нерва

· Радикулит – воспаление корешков спинного мозга

· Плексит – воспаление нервного сплетения

· Полиневрит – множественное поражение нервов

· Невралгия – болезненность по ходу нерва, не сопровождающаяся нарушением функции органа

· Каузалгия – жгучая боль по ходу нерва, возникающая после повреждения нервных стволов

· Люмбаго – острая боль, возникающая в поясничной области в момент физических нагрузок (поднятие тяжести)

· Дискогенные радикулопатии – болевые моторные нарушения, обусловленные поражением корешков спинного мозга вследствие остеохондроза позвоночника

· Миелит - воспаление спинного мозга

· Эпидурит – гнойное воспаление клетчатки в эпидуральном пространстве спинного мозга

· Сирингомиелия – образование полостей в сером веществе спинного мозга

· Полиомиелит – острое вирусное заболевание, характеризующееся поражением клеток передних рогов спинного мозга и двигательных ядер черепных нервов.

Тема: Числовые характеристики случайных величин.

Дискретная случайная величина.

Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности:
M(X) = x₁p₁ + x₂p₂ +... + x_np_n или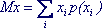

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

Пример 1. Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:

Х
p	0,2	0,5	0,3

Решение. По формуле находим математическое ожидание: M (X) = 5*0,2 + 4*0,5 + 3*0,3 = 3,3.

Свойства математического ожидания.
1) Математическое ожидание постоянной величины равно самой величине:
М(С) = С
2) Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = С·М(Х)
3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
М(Х₁ + Х₂ + …+ Х_n) = М(Х₁) + М(Х₂) +... + М(Х_n)
4) Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
М(Х₁ · Х₂ ·... · Х_n) = М(Х₁) · М(Х₂) ·... · М(Х_n)

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D (X) = M [X - M (X)]².

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)

Пример 2. Найти дисперсию случайной величины X, которая задана следующим законом распределения:

Х
p	0,3	0,5	0,2

Решение. По формуле находим математическое ожидание:

M (X) = 1*0,3 + 2*0,5 + 5*0,2 = 2,3.

Используя формулу записываем все возможные значения квадрата отклонения:

[X₁ - M (X)]² = (1 - 2,3)² = 1,69;

[X₂ - M (X)]² = (2 - 2,3)² = 0,09;

[X₃ - M (X)]² = (5 - 2,3)² = 7,29.

Тогда закон распределения квадрата отклонения имеет следующий вид:

[X - M (X)]^2	1,69	0,09	7,29
p	0,3	0,5	0,2

По формуле (3.3) находим дисперсию:

D (X) = 1,69*0,3 + 0,09*0,5 + 7,29*0,2 = 2,01.

Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

D (X) = M (X^2) - [M (X)]^2

Пример 3. Найти дисперсию случайной величины X, которая задана следующим законом распределения:

Х
p	0,1	0,6	0,3

Решение. По формуле (3.1) находим математическое ожидание:

M (X) = 2*0,1 + 3*0,6 + 5*0,3 = 3,5.

Закон распределения случайной величины X²:

Х^2
p	0,1	0,6	0,3

Математическое ожидание М(Х²):

M (X) = 4*0,1 + 9*0,6 + 25*0,3 = 13,3.

По формуле (3.4) находим дисперсию:

D (X) = 13,3 - (3,5)² = 1,05.

Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю: D(С) = 0
2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С² · D(Х)
3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х₁ ± Х₂ ±... ± Х_n) = D(Х₁) + D(Х₂) +... + D(Х_n)

Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
σ(X) = √D(X)

Дата добавления: 2014-01-04