Лекция 14. Общие вопросы теории электрических машин переменного тока

Виды электромеханических преобразователей энергии. Электрические машины переменного тока подразделяются на синхронные и асинхронные. Асинхронными электрическими машинами, прежде всего, являются самые распространенные электродвигатели, а синхронными – генераторы электрической энергии на электростанциях всех типов. В качестве электрических двигателей синхронные машины используются значительно реже, чем асинхронные. Принцип действия машин переменного тока основан на использовании вращающегося магнитного поля, создаваемого многофазными обмотками. Любая электрическая машина имеет неподвижную часть, называемую «статор», и вращающуюся часть – «ротор». У синхронных машин скорость вращения ротора постоянна при любых нагрузках и всегда равняется скорости вращения поля. У асинхронных машин скорость вращения ротора всегда отличается от скорости вращения поля. Например, у асинхронного двигателя скорость вращения ротора с увеличением момента нагрузки на валу снижается.

Электрические машины осуществляют электромеханическое преобразование энергии. В технике используются в основном три вида электромеханических преобразователей: электрический генератор; электрический двигатель; электромаг­нитный преобразователь (рис. 14.1)

Разница затрачиваемой Р _мех и полезной Р _эл мощностей является суммой потерь мощности в генераторе ∑Δ Р. Все потери мощности превращаются в теплоту, нагревающую машину.

Электрический генератор (рис. 14.1, а) преобразует механическую энергию приводящего его во вращение двигателя в элект­рическую, которая передаётся потребителю (нагрузке). Подчеркнём, что нагревание является следствием, а не причиной возникновения потерь мощности. Коэффициентом полезного действия генератора η является отношение отдаваемой активной электрической мощности к потребляемой механической.

Электрический двигатель (рис. 14.1, б) преобразует подводимую к нему электрическую энергию в механическую энергию вала, вращающегося вместе с ротором, которая используется для приведения в движение машин и механизмов (нагрузок). Этот процесс также сопровождается возникновением потерь мощности, вызывающих нагревание двигателя. КПД двигателя равен отноше­нию механической мощности на валу к потребляемой из электрической сети активной мощности.

Электромашинный преобразователь (рис. 14.1, в) преобразует электрическую энергию одного вида в электрическую энергию другого вида, например переменный ток – в постоянный, постоянный ток – в переменный, переменный ток одной частоты – в переменный ток другой частоты (преобразователь частоты) или постоянный ток одного напряжения – в постоянный ток другого напряжения (т. е. выполняет функцию трансформатора постоянного тока).

У электромеханических преобразователей энергии (электрических машин) КПД намного превосходят КПД других видов преобразователей. Например, КПД турбогенератора с номинальной мощностью 500 МВт достигает 98,75%, а КПД серийного асинхронного двигателя мощностью 3 кВт – 83%.

Магнитодвижущие силы обмоток переменного тока. Магнитодвижущая сила (МДС) всех обмоток переменного тока, расположенных на статоре или роторе электрической машины, должна создавать в ее воздушном зазоре вращаю­щееся магнитное поле. Для этого каждая из обмоток, питаю­щаяся от синусоидально изменяющегося напряжения, должна иметь МДС, синусоидально распределенную в пространстве, т. е. по расточке статора или по окружности ротора. Несо­блюдение этих условий, т. е. питание от несинусоидального напряжения или несинусоидальное распределение МДС, при­водит к появлению высших гармонических в кривой распре­деления магнитного потока, что ведет к ухудшению энергети­ческих показателей машины. Будем считать, что обмотки получают питание от источ­ника напряжения чисто синусоидальной формы. Выясним, как должна быть выполнена обмотка переменного тока, что­бы распределение её МДС было синусоидальным.

Магнитодвижущая сила сосредоточенной обмотки. Рассмот­рим двухполюсную машину с простейшей сосредоточенной обмоткой (рис.14. 2, а), у которой все витки, включенные в фазу АХ, находятся в пазах, расположенных в диамет­ральной плоскости. При прохождении тока от начала фазы А к ее концу X возникает двухполюсный магнитный поток, силовые линии которого направлены, как показано на рис. 14.2, а. Каждая силовая линия этого потока сцеплена со всеми витками w катушки данной фазы, поэтому создаваемая катушкой магнитодвижущая сила F _к = Σ i = iw.

При максимальном значении тока в катушке эта МДС также имеет максималь­ное значение: F _к = I_mw = √ 2 Iw. Примем, что вся указанная МДС расходуется на преодо­ление магнитного сопротивления воздушных зазоров, т. е. что магнитное сопротивление ферромагнитных участков магнитной цепи машины равно нулю. При этом распределе­ние МДС вдоль окружности статора имеет прямоугольную форму (рис. 14.2, б). Во всех точках воздушного зазора действует неизменная МДС: F = 0,5 F _к, при переходе через середину пазов её знак изменяется в соответствии с измене­нием полярности статора на данном участке. Прямоугольное распределение МДС можно разложить в ряд Фурье и представить в виде суммы синусоид. При этом для момента времени, соответствующего максималь­ному току в катушке, имеем:

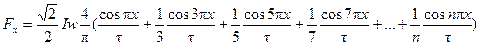, (14.1)

где х – расстояние от оси симметрии обмотки, называемой осью фазы (рис. 14.2, б).

Следовательно, при максимальном значении тока ампли­туда первой гармонической МДС для сосредоточенной об­мотки

F ₁ = (2 √ 2/π) I w ≈ 0,9 I w. (14.2)

Разложение в ряд Фурье позволяет количественно оценить отклонение кривой МДС от синусоидальной формы. При сосредоточенной обмотке это отклонение очень велико, поэтому такая обмотка получила ограниченное применение.

Магнитодвижущая сила распределенной обмотки. Для улуч­шения формы кривой распределения поля обмотку каждой фазы размещают в нескольких пазах. Это улучшает и усло­вия охлаждения обмотки. На рис. 14.3, а показана двухполюсная машина с обмоткой фазы, расположенной в шести пазах (при q = 3). Магнитодви­жущую силу распределенной обмотки можно определить как сумму МДС трех сосредоточенных катушек с числом витков в каждой w ^′ = w/ 3, сдвинутых в пространстве на угол α = π b/τ, где b – расстояние между осями соседних пазов. Форма распределения результирующей МДС получа­ется в этом случае ступенчатой (рис. 14.3, б). При максималь­ном значении тока в фазе катушки, расположенные в пазах 2 – 2 ^′, 3 – 3 ^′ и 1 – 1 ^′, создают в воздушном зазоре следующие значения МДС:

;

;.

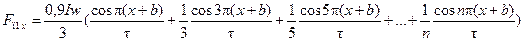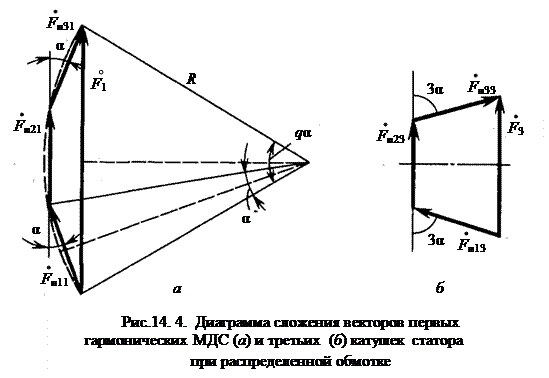
Аналитическое выражение для результирующего распреде­ления МДС обмотки можно получить суммированием МДС каждой из катушек. Наиболее удобно это сделать, изобразив векторами пространственные гармонические составляющие МДС. Амплитудные значения первой, третьей и других гармони­ческих результирующей МДС можно определить путем векторного сложения амплитуд соответствующих гармонических МДС

() отдельных катушек (рис. 14.4). При этом следует учитывать, что первые гармонические МДС () сдвинуты одна относительно другой на угол α = π b/τ, третьи – на угол 3α и т. п. Амплитудное значение первой гармонической результирующей МДС F ₁ = 2 R sin (q α/2), где R – радиус окружности, описанной вокруг векторов , определяемый из условия 2 R sin (α/2) = F _п11 = F _п21 = F _п31 = 0,9 I w.

Таким образом (рис. 14. 4, а),

F ₁ = (0,9 I w /3) sin (q α/2)/ sin (α/2), (14.3)

или в более общем виде (заменяя число 3 в знаменателе значением q)

F ₁ = 0,9 I w sin (q α/2)/[ q sin (α/2)]. (14.3 a)

Сравнивая (14.4, а) и (14.3), можно установить, что амплиту­да первой гармонической результирующей МДС при распре­делённой обмотке отличается от соответствующего значения при сосредоточенной обмотке только множителем

k _p1 = sin (q α/2)/[ q sin(α/2)], (14.4)

называемым коэффициентом распределения обмотки для пер­вой гармонической. Этот коэффициент равен отношению век­торной суммы МДС, создаваемых катушками, расположен­ными во всех пазах данной фазы, к их алгебраической сумме. При векторном сложении амплитудных значений третьих гармонических МДС катушек (рис. 14.4, б) амплитуда результирующей магнитодвижущей силы возрастает не так силь­но, как магнитодвижущая сила 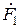, т. е. для третьих гармонических отношение амплитуд результирующей МДС к МДС одной катушки зна­чительно меньше, чем для первых гармонических. Это от­носится также ко всем высшим гармоническим МДС. Следо­вательно, распределение обмотки по нескольким пазам ослаб­ляет высшие гармонические в кривой результирующей МДС и улучшает форму поля в воздушном зазоре, приближая ее к синусоиде. В общем случае для ν -й гармонической коэффициент распределения обмотки

k _{p ν} = sin(qv α/2)/[ q sin(v α/2)], (14.5)

где v α – угол сдвига между v -ми гармоническими МДС от­дельных катушек.

Магнитодвижущая сила при укорочении шага обмотки. Из приведенных данных следует, что при распределении обмотки происходит сильное ослабление ряда высших гар­монических (пятой, седьмой). Но некоторые гармонические ослабляются незначительно. Поэтому часто наряду с рас­пределением применяют укорочение шага обмотки, т. е. расстояние у между сторонами каждой катушки берут меньшим полюсного деления τ. В этом случае обмотку выполняют двухслойной, причем одна сторона каждой катушки находится в нижнем слое, а другая – в верхнем. В качестве примера на рис. 14.5, а показано расположение двухслойной обмотки в пазах двухполюсной машины при q = 3. Обмотка каждой фазы состоит из шести катушек.

указанных обмоток (рис. 14.5, в), значение которых при максимальном значении тока в фазе. F' ₁ = F" ₁ = 0,45 Iwk _p1.

При этом

F ₁ = 2 F ^′₁ sin(πβ/2) = 0,9 Iwk _p1 k _y1, (14.6)

где k _y1 = sin(πβ/2) – коэффициент укорочения.

Для высших гармонических сдвиг по фазе между МДС двух указанных обмоток равен ν π(1 – β). При этом коэффици­ент укорочения

k _y1 = sin(νπβ/2). (14.7)

Поскольку для высших гармонических ν > 1, для некото­рых из них k _y << 1. Следовательно, укорочение шага обмоток улучшает форму распределения кривой МДС. Выбирая соот­ветствующее укорочение шага обмотки, можно полностью уничтожить одну из высших гармонических, для которой ν π(1 – β) = π.

Таким образом, распределение обмотки по нескольким па­зам и укорочение ее шага способствуют приближению кривой распределения МДС, следовательно, и кривой распределения индукции к синусоидальной форме.

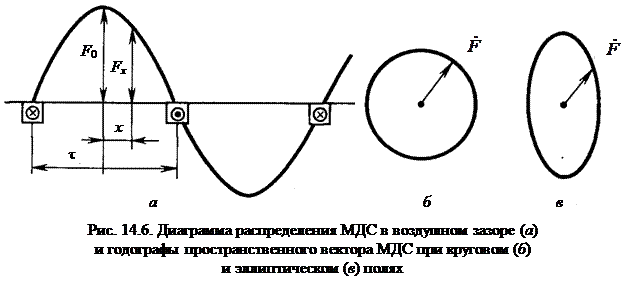
Магнитное поле электрической машины. В зависимости от типа применяемых обмоток в электри­ческой машине может возникать пульсирующее или вращаю­щееся магнитное поле (круговое или эллиптическое).

Пульсирующее поле. При питании однофазной обмотки переменным током возникает магнитное поле, пульсирующее во времени с частотой изменения тока. В этом случае при синусоидальном распределении МДС (рис. 14.6) в каждой точке воздушного зазора, расположенной на расстоянии х от оси обмотки, действует МДС

F_x = F ₀cos(π x/ τ) = F_m sinω t cos(π x/ τ), (14.8)

где F ₀ = F_m sin ω t – МДС в точке, расположенной на оси обмотки.

Выражение (8) можно привести к виду:

F_x = 0,5 F_m sin(ω t – π x/ τ) + 0,5 F_m sin(ω t + π x/ τ). (14.9)

Каждый из членов правой части (14.9) представляет собой уравнение бегущей (или вращающейся) волны МДС.

Следовательно, пульсирующее магнитное поле, синусоидально распределенное в пространстве, можно представить в виде суммы двух магнит­ных полей, вращаю­щихся в противопо­ложных направлени­ях (рис. 14.7). При этом бегущие волны МДС, создающие эти магнитные поля,

F ^′ _x = 0,5 F_m sin(ω t – π x/ τ); F ^′′ _x = 0,5 F_m sin(ω t + π x/ τ). (14.10)

в виде суммы двух векторов прямой и обратной последовательнос­тей:

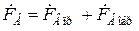(14.15)

При этом векторы и образуют систему МДС прямой последовательности, причем вектор опережает вектор на угол π/2. Векторы и 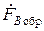образуют систему векторов МДС обратной последовательности, причем вектор 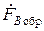отстает от вектора на угол π/2. В соответствии с порядком чередования максимумов МДС в фазах результирующее круговое магнит­ное поле прямой последовательности вращается в сторону, противоположную полю обратной последовательности. Величины векторов МДС прямой и обратной последова­тельностей определяют из уравнений (14.4–14.18), в которых значения и заменяют на 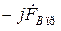и

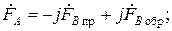
(14.16, a)

Умножая левую и правую части (17) на j, запишем:

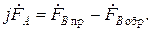(14.16, б)

Складывая уравнения (14.17, а) и (14.17, б), получают:

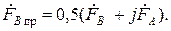(14.17)

Аналогично, вычитая (14.17, б) из (14.17, а), находят:

(14.18, а)

Из формулы (14.16) получим:

(14.18, б)

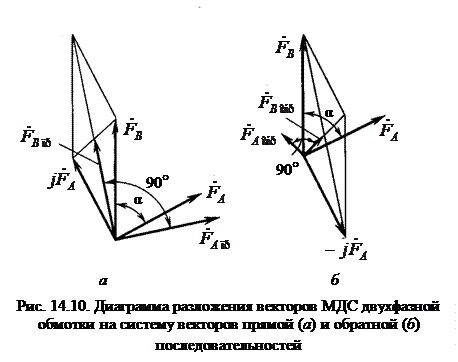
На рис. 14.10 показано графическое разложение векторов F_А и F_B на систему векторов прямой и обратной последова­тельностей в соответствии с формулами (14.17)–(14.18, б).

Так как и 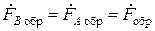, то уравнение бегущей волны для прямого и обратного круговых полей соответственно имеет вид:

F_{x пр} = F _пр sin (ω t – π x/ τ); F_{x обр} = F _обр sin (ω t + π x/ τ). (14.19)

Суммарные МДС полей, вращающихся в противополож­ные стороны, т. е. F_{x пр} и F_{x обр}, имеют различные значения (рис. 14.7, б), поэтому результирующее поле машины не пульсирующее, а вращающееся. В этом поле максимальное значение результирующей МДС в различные моменты времени не остается постоянным, как при круговом поле, т. е. поле эллиптическое. Таким образом, метод симметричных составляющих позволяет привести сравнительно сложное эллиптическое поле к двум простейшим круговым полям, вращающимся в противоположные стороны с частотой n ₁ = 60 f/p. При несимметричном питании трехфазных машин токи и МДС можно определить так же, как и в двухфазных машинах. В этом случае фазные МДС следует разлагать на три составляющие (прямой, обратной и нулевой после­довательности), из которых вращающиеся магнитные поля создают только первые две составляющие.

Дата добавления: 2014-01-04