Лекция14

Осымша

Негізгі

1. Мансұров З.А., Колесников Б.Я. Химиядағы физикалық зерттеу әдістері. - Алматы, 2002. - 166 б.

2. Мансұров З.А., Колесников Б.Я. Физикалық зерттеу әдістері.- Алматы, 1998.

3. Колесников Б.Я., Мансуров З.А. Физические методы исследования в химии. – Алматы, 2000.

4. Өтелбаев Н. Химия. – Шымкент, 2000. - Т.4.- 397 б.

5. Пентин Ю.А., Вилков Л.В. Физические методы исследования в химии – М.: Мир, 2003. – С. 684.

6. Hollas J.M Modern Spectroscopy, 4rth edn., John Wiley, Chichester, 2004.

7. Драго Р. Физические методы в химии. – М.: Мир, 1981. –Т. 1. – С. 42

8. Драго Р. Физические методы в химии. – М.: Мир, 1981. – Т. – С. 456.

9. Вилков Л.В., Пентин Ю.А. Физические методы исследования в химии // Структурные методы и оптическая спектроскопия. – М.: ВШ, 1987. – С. 368.

10. Вилков Л.В., Пентин Ю.А. Физические методы исследования в химии // Резонансные и электрооптические методы. – М.: ВШ, 1989. – С. 288.

11. Казицына Л.А., Куплетская Н.Б. Применение УФ-, ИК-, ЯМР-спектроскопии в органической химии. – М.: ВШ, 1971. – С. 264.

12. Иоффе Б.В., Костиков Р.Р., Разин В.В. Физические методы определения строения органических молекул. – Л.: ЛГУ, 1976. – С. 344.

13. Миронов В.А., Янковский С.А. Спектроскопия в органической химии. – М.: Химия, 1985. – С. 23

14. Бахшиев Н.Г. Введение в молекулярную спектроскопию. – Л.: ЛГУ, 1987. – С. 216.

15. Бенуэлл К. Основы молекулярной спектроскопии. – М.: Мир, 1985. – С. 384.

16. Браун Д., Флойд А., Сейнзбери М. Спектроскопия органических веществ. М.: Мир, 199 – С. 30

17. Сильверстейн Р., Басслер Г., Моррил Т. Спектрометрическая идентификация органических соединений. – М.: Мир, 1977. – С. 590.

18. Мальцев А.А. Молекулярная спектроскопия. – М.: МГУ, 1980. – С. 27

19. Свердлова О.В. Электронные спектры в органической химии. – Л.: Химия, 1985. – С. 248.

20. Герцберг Г. Электронные спектры и строение многоатомных молекул. – М.: Мир, 1969. – С. 77

21. Рао Ч.Н. Электронные спектры в химии. – М.: Мир, 1964. – С. 264.

22. Мейстер Т.Г. Электронные спектры многоатомных молекул. – Л.: ЛГУ, 1969. – С. 206.

23. Беллами Л. Инфракрасные спектры сложных молекул. – М.: ИЛ, 1963. – С. 300.

24. Бранд Дж., Эглинтон Г. Применение спектроскопии в органической химии. – М.: Мир, 1967. – С. 280.

25. Кесслер И. Методы инфракрасной спектроскопии в химическом анализе. – М.: Мир, 1964. – С. 286.

26. Наканиси К. Инфракрасные спектры и строение органических соединений. – М.: Мир, 1965. – С. 216.

27. Прикладная инфракрасная спектроскопия // Под ред. Д. Кендалла – М.: Мир, 1970. – С. 250.

28. Смит А. Прикладная инфракрасная спектроскопия: основы, техника, аналитическое применение. – М.: Мир, 198 – С. 328.

29. Ионин Б. И., Ершов Б. А., Кольцов А.И. ЯМР-спектроскопия в органической химии. – Л.: Химия, 1988. – С. 270.

30. Попл Дж., Шнейдер В., Берстейн Г. Спектры ядерного магнитного резонанса высокого разрешения. – М.: ИЛ, 196 – С. 59

31. Робертc Дж. Ядерный магнитный резонанс. – М.: ИЛ, 1961. – С. 250.

32. Керрингтон А., Мак-Лечлан Э. Магнитный резонанс и его применение в химии. – М.: Мир, 1970. – С. 448.

33. Жунке А. Ядерный магнитный резонанс в органической химии. – М.: Мир, 1974. – С. 176.

34. Лундин А.Г., Федин Э.И. ЯМР-спектроскопия. – М.: Наука. 1986. – С. 224.

35. Эрнст Р., Боденхаузен Дж., Вокаун А. ЯМР в одном и двух измерениях. – М.: Мир. 1990. – С. 710.

36. Эмсли Дж., Финей Дж., Сатклиф Л. Спектроскопия ЯМР высокого разрешения. – М.: Мир, 1968. Т. 1. – С. 630.

37. Эмсли Дж., Финей Дж., Сатклиф Л. Спектроскопия ЯМР высокого разрешения. – М.: Мир, 1969. Т. – С. 468.

38. Kettle, S. F. A. Symmetry and Structure, 2nd edn, John Wiley, Chichester.,1995.

39. Duxbury, G. Infrared Vibration–Rotation Spectroscopy, John Wiley, Chichester., 1999.

40. Long, D. A. The Raman Effect, John Wiley, Chichester., 200

41. Bunker, P. R. and Jensen, P. Molecular Symmetry and Spectroscopy, 2nd edn., NRC Press, Canada, 1998.

42. Вертц, Д. Болтон Д. Теория и практическое приложение метода ЭПР. – М.: Мир, 1975. – С. 207.

43. Герсон Ф., Спектроскопия ЭПР высокого разрешения, – М., Мир, 1977, – C. 193.

44. Полякова А.А., Хмельницкий Р.А. Введение в масс-спектрометрию органических соединений. – Л.: Химия, 1966. – С. 203.

Рассматриваемые вопросы:

1) Общая схема проверки статистических гипотез.

2) Сравнение выборочной средней с гипотетической средней нормальной совокупности.

3) Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности.

4) Сравнение двух дисперсий нормальных генеральных совокупностей.

5) Критерий согласия Пирсона хи-квадрат.

1) Общая схема проверки статистических гипотез.

Определение 1. Статистической гипотезой называется любое высказывание о конкретных значениях параметров распределения некоторой случайной величины или о виде этого распределения.

В первом случае гипотеза называется параметрической, во втором- непараметрической.

При проверке статистической гипотезы прежде всего необходимо сформулировать основную или нулевую гипотезу 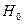. Различают простые и сложные гипотезы.

Определение 2. Гипотеза называется простой, если она состоит в равенстве одного или нескольких параметров заданным числам.

Если множество допустимых для справедливости гипотезы значений параметров состоит более чем из одного элемента, то ее называют сложной.

Например,

простые гипотезы,

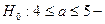сложная гипотеза.

Одновременно с нулевой гипотезой рассматривается некоторая гипотеза, называемая альтернативной или конкурирующей. Ее обычно обозначают 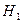. Различают односторонние и двусторонние конкурирующие гипотезы. Например,

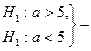односторонние гипотезы,

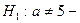двусторонняя гипотеза.

Выбор вида альтернативной гипотезы определяется смыслом задачи.

Для проверки нулевой гипотезы используют специальным образом подобранную случайную величину (статистический критерий, или еще говорят, статистику). В зависимости от вида распределения критерий обозначают через (если он распределен нормально), 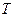(если он распределен по закону Стьюдента), (если он распределен по закону Фишера-Снедекора) и т.д. В целях общности будем обозначать статистический критерий через 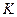. Наблюдаемым значением критерия 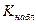называют значение критерия, вычисленное по выборке.

После выбора критерия множество всех его возможных значений разбивают на два подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается (критическая область), а другое содержит те значения критерия, при которых нулевая гипотеза принимается (область принятия гипотезы). Основной принцип проверки статистических гипотез можно сформулировать так: если 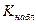принадлежит критической области, то нулевую гипотезу отвергают в пользу конкурирующей гипотезы 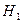; если 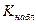принадлежит области принятия гипотезы, то нулевую гипотезу 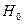принимают. При этом возможны четыре случая:

Гипотеза	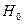Принимается	Отвергается
Верна	Правильное решение	Ошибка 1-го рода
Не верна	Ошибка 2-го рода	Правильное решение

Вероятность 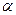допустить ошибку 1-го рода, т.е. отвергнуть гипотезу 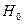, когда она верна, называется уровнем значимости критерия.

Вероятность допусить ошибку 2-го рода, т.е. принять гипотезу 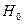, когда она не верна, обозначается через 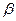. Вероятность 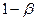не допустить ошибку 2-го рода называется мощностью критерия.

Вероятности ошибок 1-го и 2-го рода определяются выбором критической области.

Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области. Точки , которые разделяют критическую область и область прнятия решения, называют критическими точками.

Правосторонней называют критическю область, определяемую неравенством 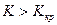, где .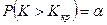

Левосторонней называют критическю область, определяемую неравенством 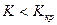, где .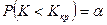

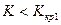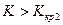Двусторонней называют критическую область, определяемую двумя неравенствами и , где 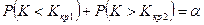. Для симметричного относительно нуля критерия полагают , .

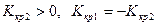Для каждого из используемых критериев имеются таблицы, по которым по уровню значимости критерия разыскиваются критические точки.

Выбор критических точек поясним на примере правосторонней критической области. Пусть уровень значимости 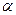критерия выбран и по нему определена критическая точка . Допустим, что 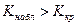. Тогда мы нулевую гипотезу 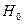отклоняем. Отклоненная гипотеза может быть истинной, а может быть ложной. Поскольку 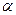мало, ошибка 1-го рода (отклонить верную гипотезу) практически невозможна. Поэтому отклоненная гипотеза 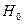ложна.

Наиболее просто общая схема проверки статистических гипотез может быть проиллюстрирована на примере простых гипотез, что, фактически, делается с помощью доверительных интервалов для соотсетствующих параметров.

Дата добавления: 2014-01-04