Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности

Пусть случайная величина 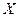распределена нормально, но ее дисперсия 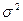неизвестна. Предположим, что из некоторых соображений можно предположить, что ее значение есть 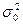. Требуется по исправленной дисперсии при заданном уровне значимости 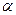проверить нулевую гипотезу 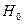: 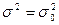. Исправленная дисперсия 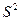является несмещенной оценкой дисперсии 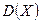случайной величины 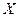. Поэтому нулевую гипотезу 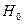можно записать так: .

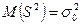Для проверки нулевой гипотезы 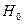используют критерий

,

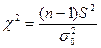где 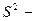исправленная выборочная дисперсия.

Для того, чтобы при заданном уровне значимости 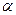проверить нулевую гипотезу, нужно вычислить наблюдаемое значение критерия .

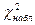1) При конкурирующей гипотезе 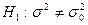критическая область является двусторонней и определяется двумя критическими точкам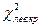и и 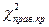. Критические точки находят по таблице критических точек распределения 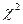с 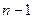степенями свободы: 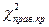при уровне значимости 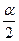, 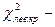при уровне значимости .

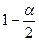Если 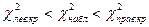, то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

2)При конкурирующей гипотезе 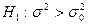критическую точку 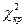правосторонней критической области находят по таблице критических точек распределения 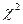с 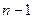степенями свободы при уровне значимости .

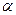Если 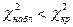, то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

3) При конкурирующей гипотезе критическую точку 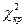левосторонней критической области находят по таблице критических точек распределения 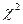с 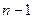степенями свободы при уровне значимости .

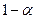Если 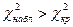, то нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают.

Дата добавления: 2014-01-04