Соединённых невосстанавливаемых элементов

Система из независимых последовательно

Произвольное распределение времени работы до отказа

Предполагается, что все элементы системы (объекта) взаимно независимы, т.е. отказ любого элемента никак не зависит от состояния любых других элементов системы.

Кроме того, предполагается, что известны выражения для вероятности безотказной работы отдельных элементов 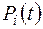или оценки для этих функций.

Если система состоит из n отдельных элементов с показаниями безотказности 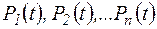, то вероятность безотказной работы системы за время t находят по формуле

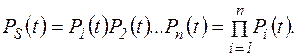(5.7)

Чем больше число элементов n, тем при прочих равных условиях 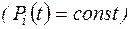меньше вероятность безотказной работы систем .

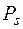Среднюю наработку системы до отказа (математическое ожидание наработки до отказа) найдем по формуле

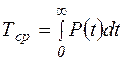(5.8)

или по формуле

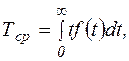(5.9)

где 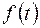– плотность распределения наработки системы до отказа; в общем случае 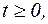а при 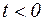принимается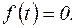

Функцию распределения наработки до отказа определяют по формуле

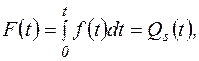(5.10)

где 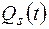– вероятность отказа системы за время t.

Вероятность безотказной работы системы в течение наработки t находят по формуле

(5.11)

Время работы до отказа системы из n последовательно соединенных невосстанавливаемых элементов определяется минимальным значением времени безотказной работы ее элементов, т.е.

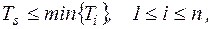(5.12)

где 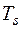– время работы системы до отказа; 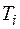– время работы до отказа i -го элемента.

Иначе говоря, время работы до отказа системы из n последовательно соединенных невосстанавливаемых элементов не может быть больше времени безотказной работы самого ненадежного элемента.

Основные динамические модели (показатели) надёжности для систем из последовательно соединенных невосстанавливаемых элементов при произвольных распределениях времени работы до отказа, т. е. при произвольных функциях 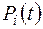, имеют вид

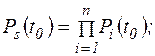
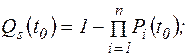
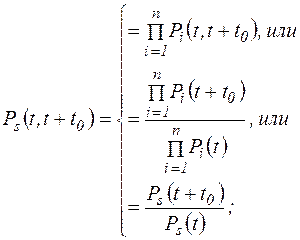(5.13)

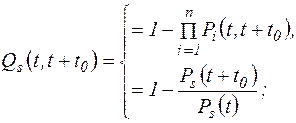
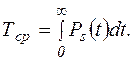
В отличие от динамических моделей их статические аналоги примут вид 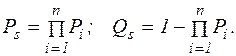(5.14)

Если для всех подсистем значения 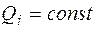одинаковы, то 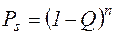. (5.15)

Нормальное распределение

Плотность распределения наработки системы до отказа имеет вид

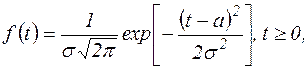
где а и s – параметры распределения, a > 0, s > 0, s/a < 0,25.

Последнее условие является необходимым, если для положительной случайной величины вместо усеченного нормального распределения приближенно использовать нормальное распределение.

Вероятность безотказной работы находят по формуле

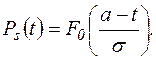(5.16)

Значения вероятности безотказной работы в зависимости от 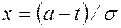приведены в специальных таблицах.

Среднюю наработку до отказа находят по формуле

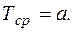(5.17)

Вероятность отказа системы за время t находят по формуле

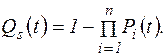(5.18)

Вероятность безотказной системы в интервале времени от t до t + t₀ определим по формуле

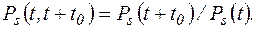(5.19)

Тогда вероятность отказа системы в интервале времени от t до t + t₀ находим по формуле

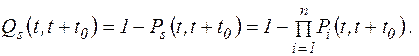(5.20)

Если наработка системы до отказа распределена по нормальному закону с параметрам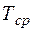и и 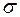, то наработка, отвечающая вероятности безотказной работы 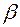, находится по уравнению

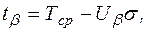(5.21)

где 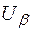– квантиль нормального распределения, отвечающий вероятности .

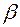Интенсивность отказов системы, имеющей нормальное распределение наработки до отказа, находят по формуле

(5.22)

где – табулированная функция.

Пример 5.5.

Наработка невосстанавливаемой системы до отказа подчиняется нормальному распределению с параметрам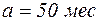и и .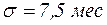

Требуется найти:

1) вероятность безотказной работы для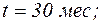

2) среднюю наработку до отказа;

3) наработку на отказ, отвечающую вероятности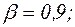

4) интенсивность отказов для ряда значений наработки: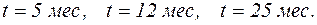

Решение

1. Вероятность безотказной работы за время :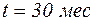

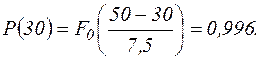
2. Средняя наработка до отказа составит: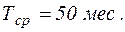

3. Наработка на отказ, отвечающая вероятности 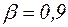, имеет вид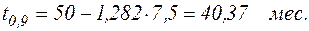

4. Интенсивность отказов:

для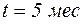

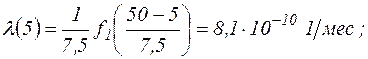
для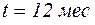

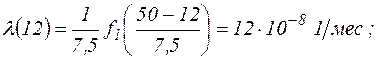
для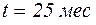

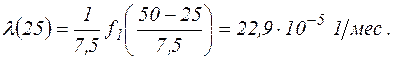
Дата добавления: 2014-01-04