Вынужденные электрические колебания

Чтобы колебания в контуре не затухали необходимо периодически пополнять энергию. Для этого в контур включают переменную ЭДС, которая изменяется по гармоническому закону

= _оcos w_вt. (8.19)

Электрические колебания в контуре (рис. 8.2) описываются формулой (8.4)

, (20)

или

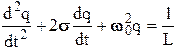
_о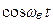. (8.21)

Решение такого неоднородного дифференциального уравнения представляет собой сумму общего решения однородного уравнения (8.10) и частного решения уравнения (8.21).

В случае установившихся электрических колебаний рассматривают только частное решение, так как решение однородного уравнения обращается в нуль (колебания затухают).

Частное решение запишем в виде при (w=w_в)

q = q_o cos (wt -g), (8.22)

где q_o - амплитудное значение заряда на конденсаторе; g - разность фаз между колебаниями заряда и, вынуждающей ЭДС.

Причем q_o и g определяются свойствами контура и вынуждающей ЭДС (g > 0, поэтому q всегда отстает по фазе от ЭДС ).).

Задача заключается в нахождении q_o и g. Сначала найдем уравнение колебания тока. Дифференцируя (8.22) по времени t, имеем

I = - wq_osin(wt - g) = wq_ocos(wt - g + )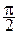

или

I = I_o cos(wt - j), (8.23)

где I_o = wq_o - амплитудное значение тока; j - сдвиг по фазе между током и внешней ЭДС, т. е.

j = g -.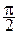

Представим уравнение (8.20) в виде

U_R + U_C + U_L = _оcoswt, (8.24)

где

U_R = IR = R I_o cos(wt - j), (8.25)

U_C=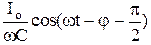, (8.26)

U_L = wL I_o cos(wt - j + 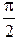), (8.27)

Из уравнений (8.25), (8.26), (8.27) следует, что U_R находится в фазе с током I;

U_C отстает по фазе от I на 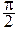; U_L опережает ток на.

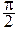  Рис. 8.5

Это можно наглядно представить с помощью векторной диаграммы (рис. 7.5), если амплитуды напряжений представить в виде

U_Rо = R I_o, U_Cо= , U_LО = wLI_o,

т. е. их векторная сумма равна вектору величины _О.

Используя рис. 8.5 найдем выражения для I_o и j:

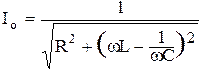
_о, (8.28)

. (8.29)

Дата добавления: 2014-01-04