Преобразование матрицы жесткости при переходе от одной системы координат к другой

Обычно матрицу жесткости строят в удобной для данного элемента системе координат, которую принято называть локальной или местной. При переходе от отдельных элементов к системе элементов необходимо осуществить переход от локальных систем координат к общей для всех элементов системе координат, которую принято называть глобальной.

Пусть известны перемещения какого-либо жесткого узла k элемента в локальной системе координат, оси которой 1` и 2` повернуты на угол j относительно осей 1 и 2 глобальной системы координат. Оси 3 и 3`, очевидно, будут совпадать, т.к. в обоих случаях рассматривается одна и та же плоскость (рис.17.15).

Пусть 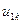и - перемещения узла k по направлению 1 в глобальной и локальной системах координат соответственно, а 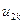и - перемещения по направлению 2 в глобальной и локальной системах координат соответственно.

Из рис.17.15 следует:

,

.

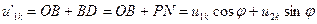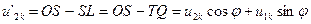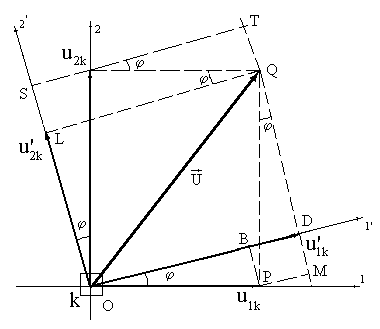
Рис.17.15

Очевидно, угловое смещение в обоих системах осей координат будет одинаковым, т.е. . Полученные соотношения, связывающие перемещения узла в локальной и в глобальной системах координат, в матричной форме будут выглядеть следующим образом:

.

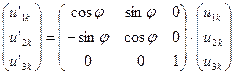Матрица 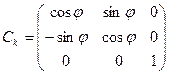называется матрицей направляющих косинусов для k -го узла. Легко убедиться, что элемент, стоящий в ее i -ой строке и j -ом столбце равен косинусу угла между i -ой осью в локальной системе координат и j -ой осью в глобальной системе координат.

Для шарнирного элемента связь между перемещениями в локальной и глобальной системах осей будет аналогичной:

.

Для элемента, содержащего несколько узлов, связь между вектором узловых перемещений U в глобальной системе осей координат и вектором узловых перемещений U` в локальной системе осей координат осуществляется при помощи квазидиагональной матрицы направляющих косинусов C^(e) элемента, составленной из матриц направляющих косинусов входящих в элемент узлов:

. (17.4)

Например, для элемента, изображенного на рис.9.9, выражение (9.4) будет выглядеть следующим образом:

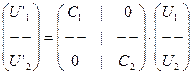
или

.

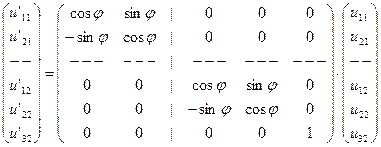Легко убедиться, что это равенство соответствует уравнениям, связывающим перемещения в локальной и глобальной системах осей координат:

,

,

,

,

.

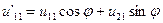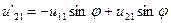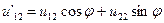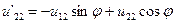Повторив те же рассуждения для усилий, действующих на узлы элемента, получим аналогичную (17.4) зависимость между векторами усилий, действующих на элемент, построенных для глобальной системы координат 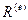и для локальной системы координат :

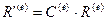(17.5)

Усилия, действующие на узлы элемента и узловые перемещения связаны зависимостью (9.2). Запишем ее также и для локальной системы осей координат:

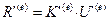. (17.6)

Заменим в (17.6) вектора усилий и перемещений согласно зависимостям (17.4) и (17.5):

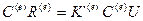и умножим получившееся равенство слева на матрицу , т.е. на матрицу, обратную матрице направляющих косинусов элемента: . Сопоставляя это выражение с (17.2), получим зависимость, связывающую матрицы жесткости, построенные в глобальной и локальной системах координатных осей: 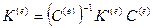. Известно, что у матрицы направляющих косинусов обратная матрица совпадает с транспонированной матрицей. Поэтому, окончательно получаем:

. (17.7)

Итак, если матрица жесткости элемента построена в локальной системе осей координат, то по формуле (9.7) можно получить из нее матрицу жесткости элемента в глобальной системе осей координат.

Дата добавления: 2014-01-04