Пример расчета стержневой системы методом конечных элементов

Выполним методом конечных элементов расчет системы, изображенной на рис.17.31. Как уже отмечалось, МКЭ - метод, ориентированный на использование ЭВМ. Объем вычислений при реализации этого метода, как правило, значительно превышает объем вычислений, который приходится проделывать при расчете систем с использованием классических методов строительной механики. Поэтому использование МКЭ при расчетах вручную имеет смысл только в учебных целях для лучшего усвоения учащимися процедуры метода.

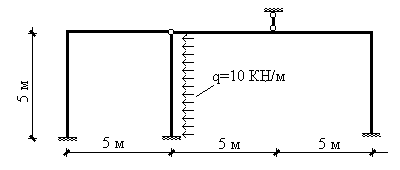
Рис.17.31

Сечения всех стержней системы заданы одинаковыми и характеризуется жесткостью на растяжение - сжатие EF =10⁶ кН и жесткостью на изгиб EI =40×10⁶ кН×м². Как известно, при силовых воздействиях распределение усилий в стержневых системах зависит от распределения жесткостей, а не от их абсолютных величин. Поэтому, для удобства расчетов будем задавать EF =1 кН и EI =40 кН×м². Полученные в результате расчета усилия от этого не изменятся, а полученные в результате расчета перемещения нужно будет уменьшить в 10⁶ раз.

Заменим исходную стержневую систему конечно-элементной моделью, узлы и элементы пронумеруем (рис.17.32).

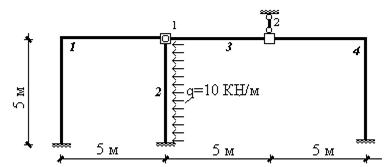
Рис.17.32

Перейдем от исходной нагрузки к узловой. Закрепим узлы конечно-элементной схемы от смещений, найдем реакции во введенных связях и построим эпюру изгибающего момента в стержнях системы, т.е. решим задачу 1 (рис.17.33). Поскольку внешняя нагрузка действует только на элемент 2, достаточно рассмотреть только этот элемент (рис.17.34). Воспользовавшись табличным решением, построим эпюру изгибающего момента и определим усилия, действующие со стороны элемента на узел (рис.9.34). На стержнях остальных элементов эпюра моментов будет отсутствовать.

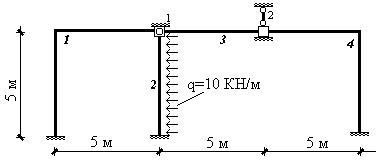
Рис.17.33

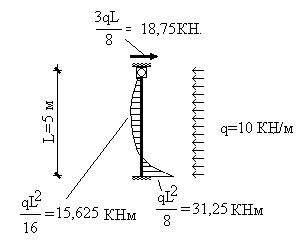
Рис.17.34

Во введенных связях будет действовать только одна реакция - горизонтальное усилие в узле 1, равное 18,75 кН.

Перейдем теперь к решению задачи 2. Узловая нагрузка определяется как реакции во введенных связях в задаче 1, взятые с обратным знаком. В нашем случае в качестве нагрузки будет фигурировать только горизонтальное усилие в узле 1 (рис.17.35).

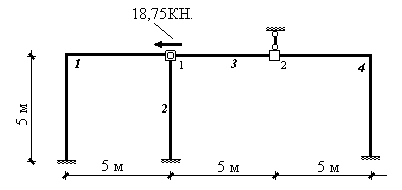
Рис.17.35

Следовательно, вектор внешней нагрузки Р будет следующим:

.

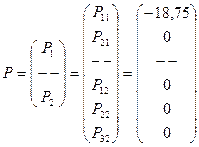Теперь построим матрицы жесткости всех элементов системы. Вопрос построения матриц жесткости был подробно рассмотрен выше, поэтому здесь приведем только построенные матрицы жесткости в глобальной системе координат:

,

,

,

.

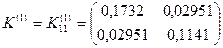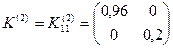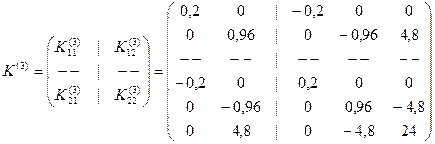Следующим шагом является формирование глобальной матрицы жесткости в соответствии с формулой (17.11):

.

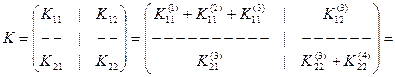
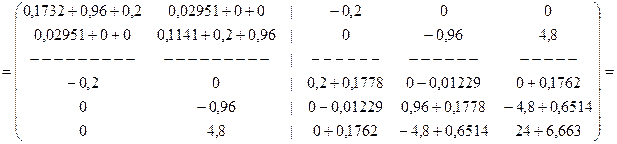
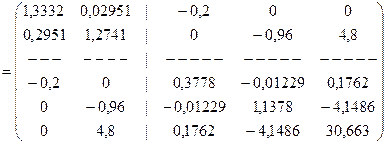Составим теперь систему разрешающих уравнений (17.10) метода конечных элементов:

.

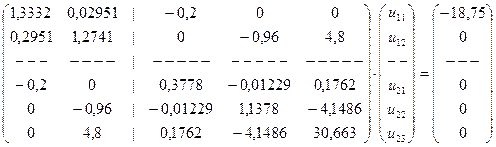Поскольку на перемещение узла 2 по направлению 2 наложено ограничение, в эту систему внесем необходимые изменения:

.

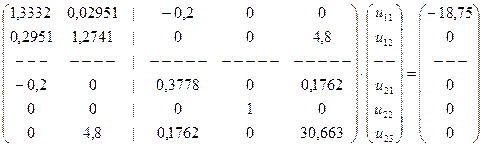Решив полученную систему линейных алгебраических уравнений, получим вектор узловых перемещений:

.

Напомним, что истинные перемещения в системе будут в 10⁶ раз меньше полученных.

Далее, необходимо определить усилия, действующие на каждый элементы системы со стороны узлов, для чего воспользуемся формулой (17.2):

,

,

;

.

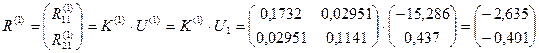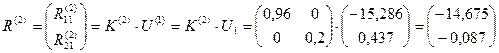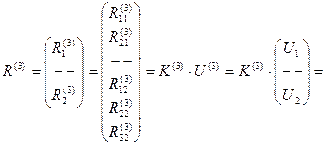
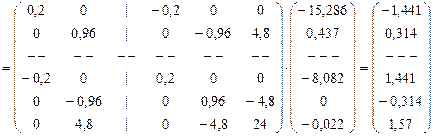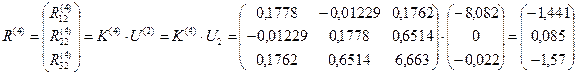Компоненты полученных векторов представляют собой усилия, действующие на узлы элементов. На данном этапе следует выполнить промежуточную проверку равновесия элементов и узлов под действием этих сил и внешней узловой нагрузки (рис.9.36).

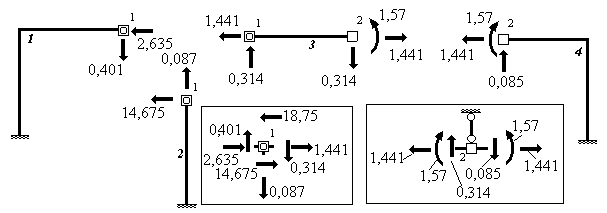
Рис.17.36

Теперь, зная приложенные к узлам элементов усилия (рис.17.36), построить эпюру изгибающих моментов в стержнях системы не составит труда (рис.17.37). На этом решение задачи на действие только узловой нагрузки (задачи 2) заканчивается. Для построения окончательной эпюры моментов необходимо сложить решение этой задачи (задачи 2) и решение задачи 1 (рис.17.38).

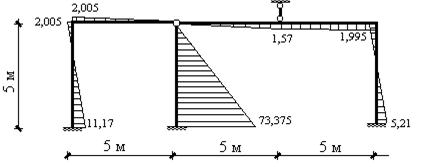
Рис.17.37

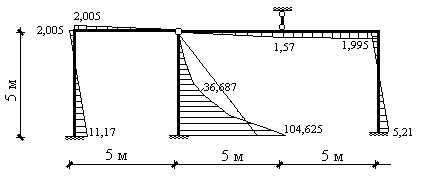
Рис.17.38

Далее, как обычно, остается построить эпюры поперечного и продольных усилий, а также выполнить статическую и деформационную проверки. Эти операции предлагается проделать самостоятельно.

Дата добавления: 2014-01-04