Простейшие свойства полей

Каждое поле является коммутативным кольцом. Поэтому все свойства коммутативных колец присущи и любому полю; все утверждения доказанные для коммутативных колец, справедливы также и для всякого поля.

Рассмотрим простейшие свойства полей, вытекающие из выполнимости операции деления. Из определения поля и свойств его групп вытекают следующие свойства.

Теорема. В каждом поле существует, и притом только одна, единица.

Доказательство. По определению поля, в поле существует, по крайней мере один, отличный от нуля элемент 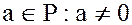. Так как в поле выполнима операция деления, кроме деления на нуль, то в нем существует частное .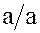

Обозначим его символом .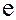

Тогда .

Пусть 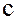– произвольный элемент поля . Покажем, что 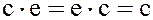. Если , то это означает, что в поле существует такой элемент , что .

Следовательно, , т.е. , и поэтому – единичный элемент поля . Единичный элемент 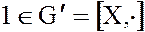. В соответствии с теоремой о единичном элементе группы – он единственен.

Теорема. В каждом поле деление на любой ненулевой элемент возможно и притом единственным способом.

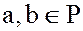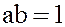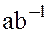Доказательство. Пусть , причем , а , тогда Произведение записывается в виде дроби 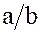и является единственным решением уравнения – частное от деления на .

Теорема. В каждом поле для любого его элемента , отличного от нуля, существует, и притом только один, обратный элемент .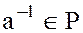

Доказательство. Действительно, в любом поле существует частное 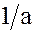элементов и . Обозначим это частное символом 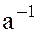. Тогда .

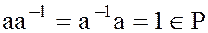Теорема. Любое поле не содержит делителей нуля: .

Доказательство. Пусть и . Тогда если и, следовательно, . С другой стороны, если .

Замечание. Из этой теоремы следует, что произведение отличных от нуля элементов и поля также отлично от нуля. Следовательно, операция умножения элементов поля 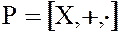определена также и на множестве отличных от нуля элементов этого поля.

Теорема. В каждом поле 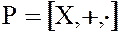множество отличных от нуля элементов является абелевой группой относительно умножения – .

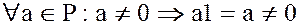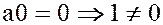Доказательство. Действительно, на множестве определена операция умножения, а так как , то эта операция ассоциативна и коммутативна. Так как , а . Поэтому единичный элемент . Если 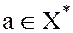, т.е. если , то 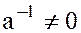, поскольку , а и, следовательно, .

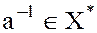Определение. Мультипликативную группу , состоящую из всех отличных от нуля элементов поля , называется мультипликативной группой поля .

Так как отличные от нуля элементы поля образуют мультипликативную абелеву группу поля , то все свойства мультипликативной группы присущи полю . В частности, в каждом поле можно выполнять сокращение на множитель, отличный от нуля: если .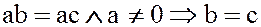

В любом поле сохраняются обычные правила действия над степенями элементов с целыми показателями:

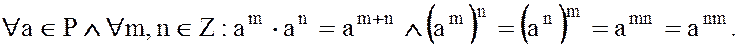
Теорема. В любом поле для любых 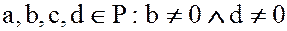частные (дроби) подчиняются следующим правилам:

1. тогда и только тогда, когда ;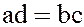

2. ;

3. ;

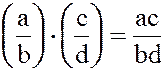4. ;

5. ;

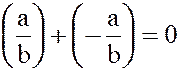6. .

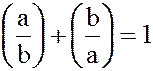Это обычные «школьные» правила, но они строго выводятся из аксиом поля.

Доказательство. Докажем первое равенство. Пусть и 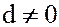, тогда в поле существуют обратные элементы 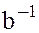и такие, что если

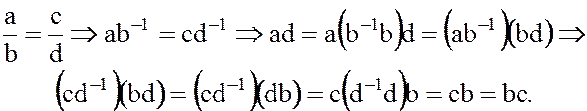
Этим доказана необходимость условия.

Докажем достаточность этого условия. Предположим, что 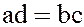. Умножив обе части этого равенства на , имеем

Докажем второе равенство:

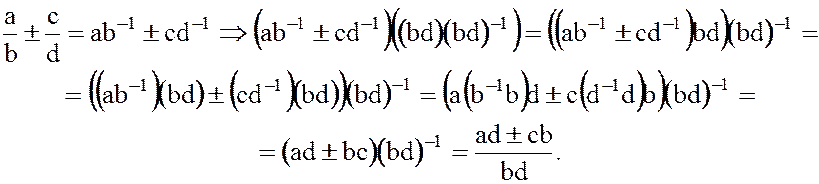
Докажем третье равенство:

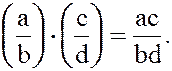
Действительно:

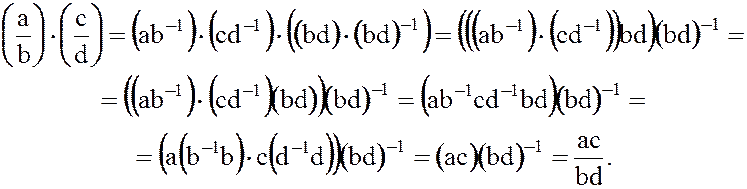
Докажем четвертое равенство:

Действительно:

Докажем пятое равенство. Действительно,

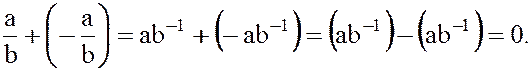
Докажем шестое равенство. Действительно,

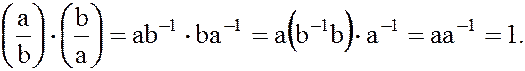
Рассмотренные свойства полей позволяют сделать вывод о том, что в любом числовом поле верны все утверждения и формулы элементарной алгебры, базирующиеся на правилах действия над степенями с целыми показателями и над частными (дробями).

Рассмотрим пример не числового поля 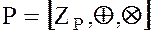– поля классов вычетов по модулю .

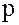Теорема. Кольцо классов вычетов является полем тогда и только тогда, когда 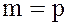– простое число.

Теорема будет доказана если мы покажем, что при 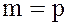выполняются следующие условия:

1. Множество классов вычетов – 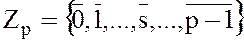– не содержит делителей нуля;

2. .

Доказательство. Пусть 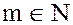– не простое число. Это означает, что 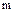можно представить в виде , тогда . Это означает, что и являются делителями нуля в .

Пусть 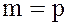– простое число, тогда, множество классов вычетов принимает вид:

(4.2)

Обозначим все элементы множества отличные от нуля :

(4.3)

Эти элементы образуют конечную мультипликативную группу: операция умножения на множестве ассоциативна и существует единичный элемент, равный . Обозначим эту группу .

Рассмотрим отображение 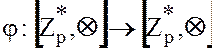конечной мультипликативной группы саму на себя, которое определим

,

где 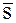произвольный, но фиксированный элемент из .

Применяя отображение 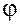к множеству из (4.3) получаем множество

(4.4)

Все элементы множества (4.4) отличны от нуля и все различны: 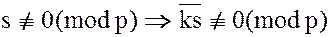при

Предложим обратное. Если 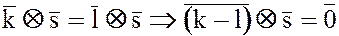, это возможно только при .

Это означает, что последовательность (4.4) совпадает с переставленной некоторым образом последовательностью (4.3), а это означает, что в последовательности (4.4) . Это означает, что является обратным к а т.к. – произвольный элемент из , то это и доказывает теорему.

Следствие 1. (малая теорема Ферма). Для любого целого 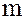не делящегося на простое 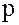имеет место сравнение

. (4.5)

Доказательство. 1. Мультипликативная группа имеет порядок .

По теореме Лагранжа порядок этой группы делится на порядок любого элемента из группы .

2. Из следствия т. Лагранжа следует, что группа простого порядка всегда циклическая, а порядок любого элемента циклической группы совпадает с порядком группы.

Следовательно, любой элемент 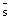группы 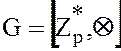в степени будет равен единичному элементу т.е. .

С другой стороны если 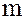не делится на 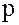, то его можно представить в виде , где т.е. совпадает с одним из элементов группы .

Следовательно,

.

Следствие 2. Для любого целого 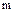имеет место сравнение

(4.6)

Доказательство. Действительно, умножая обе части сравнения (4.5) на 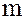, получим

.

Этот результат имеет место и тогда, когда числа 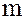и 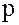не являются взаимно простыми. Есл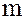и и 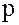не взаимно простые числа, то при простом 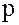число 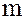делится на 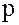. Но тогда 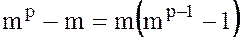также делится на 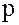. Поэтому 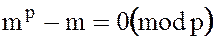или .

Пример. Найти остаток от деления числа 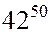на 17. Поскольку 17 и 42 взаимно простые числа, то по малой теореме Ферма 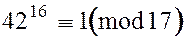. Возводя в третью степень обе части сравнения, получаем 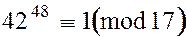. Кроме того, , а в квадрате это дает . Перемножая полученные сравнения, находим 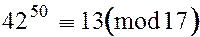. Таким образом, искомый остаток равен 13.

Дата добавления: 2014-01-04