Обобщенные координаты и число степеней свободы

Лекция IV-ОАМ-12

Обобщенные координаты. Связи и их уравнения. Классификация связей. Виртуальные перемещения. Идеальные связи.

ГЛАВА XVII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ

Перемещения точек несвободной механической системы не могут быть совершенно произвольными, так как они ограничены имеющимися связями. Это означает, что не все координаты точек независимы. При таком условии положение точек системы определяется заданием только независимых координат. Остальные координаты определяются из уравнений связей (см. § 21.).

Независимые величины, заданием которых однозначно определяется положение всех точек механической системы, называются обобщенными координатами этой системы. Для голономных систем число независимых обобщенных координат механической системы равно числу степеней свободы этой системы.

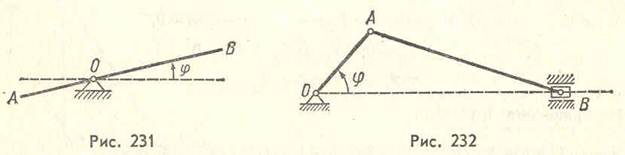
Так, например, положение рычага АВ с осью вращения О (рис. 231) вполне определяется заданием его угла поворота φ. Угол φ можно рассматривать как обобщенную координату рычага. Так как положение рычага определяется одной обобщенной координатой, то рычаг имеет одну степень свободы.

Положение всех точек кривошипного механизма (рис. 232) вполне определяется заданием только угла поворота кривошипа φ. Этот угол можно принять за обобщенную координату этой системы, имеющую также одну степень свободы.

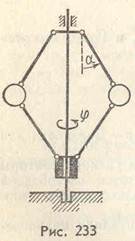Положение всех точек центробежного регулятора (рис. 233), вращающегося вокруг вертикальной оси, определяется заданием угла поворота регулятора φ и угла α, образованного каждым из стержней с вертикалью. Не зависящие друг от друга углы φ и α можно считать обобщенными координатами. Так как положение регулятора определяется двумя обобщенными координатами, то он имеет две степени свободы.

Положение свободной материальной точки в пространстве определяется тремя декартовыми координатами, не зависимыми друг от друга. Поэтому свободная материальная точка имеет три степени свободы.

Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, так как его положение определяется только углом поворота ф.

Тело, совершающее сферическое движение, имееттри степени свободы, так как его положение определяется тремя эйлеровыми углами ψ, θ, φ.

Свободное твердое тело, движение которого определяется шестью уравнениями, имеет шесть степеней свободы. Механическая система, положение которой определяют s обобщенных координат, имеет S степеней свободы.

Декартовы координаты любой точки М_i механической системы являются функциями обобщенных координат этой системы. Так, например, зная длину кривошипа r и длину шатуна l кривошипно-шатунного механизма (рис. 234), можно выразить декартову координату ползуна В через обобщенную координату φ: или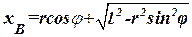

Таким же образом можно определить координату любой точки этого механизма.

Обозначим 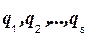обобщенные координаты механической системы, имеющие S степеней свободы. Декартовы координаты любой точки M_i этой системы при стационарных связях являются функциями S обобщенных координат:

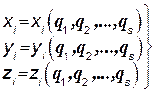(112.1)

При наличии нестационарных связей декартовы координаты всех точек механической системы являются функциями не только обобщенных координат q, но и времени t:

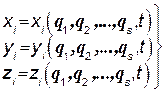(112.2)

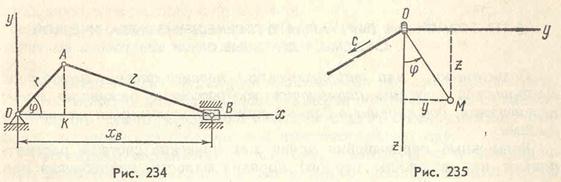
Например, при переменной длине нити маятника ОМ=l =l₀ - ct (рис. 235), точка М имеет координаты:

y=(l₀-ct)sinφ, z==(l₀-ct)cosφ.

Эти координаты зависят не только от обобщенной координаты φ, но и от времени t.

Дата добавления: 2014-01-04