Линейные операторы

Лекция 8

Вычисляются коэффициенты автокорреляции, автокавариации и частичной автокорреляции.

Уменьшается время получения значений стохастического ряда сравнительно с имитационным моделированием в 10-100 раз (в зависимости от вида процесса).

Методика реализуется так:

1. Строится приближенная модель ряда желаемой размерности.

3. Осуществляется итерактивный процесс за методом наименьших квадратов.

4. Находится остаточная сумма квадратов разниц между приданными значениями ряда и значениями, что получены с помощью построенной модели.

5. Уточняются коэффициенты модели.

6. Если точность не достигнута, то опять выполняются пункты 1 и 2.

7. Находится необходимое количество прогнозов, которые возможно использовать как последующие значения стохастического ряда.

Автор(и): Фамилия, имя, отчество

Тема: “ Линейные операторы ”

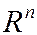Определение 1. Если задан закон (правило). По которому каждому вектору пространства ставится в соответствие единственный вектор 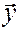пространства 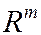, то говорят, что задан оператор (преобразование, отображение) 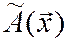, действующий из 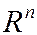в 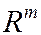, и записывают 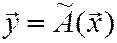. При этом вектор 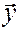называют образом вектора , а сам вектор - прообразом вектора .

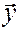Определение 2. Оператор 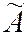называется линейным, если для любых векторов и 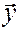пространства 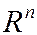и любого числа 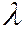выполняются соотношения:

1) 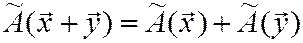- свойство аддитивности оператора;

2) 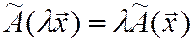- свойство однородности оператора.

Если пространства 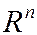и 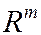совпадают, то оператор 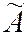отображает пространство 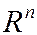в себя. Далее будем рассматривать такие операторы.

Выберем в пространстве 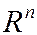базис 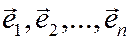. Запишем разложение произвольного вектора по данному базису:

.

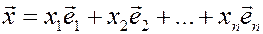В силу линейности оператора 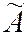получаем

.

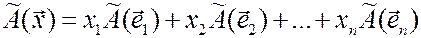Так как (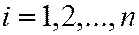) также вектор из 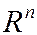, то его можно разложить по базису 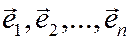. Пусть

().

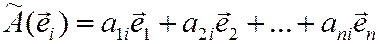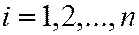Таким образом,

.

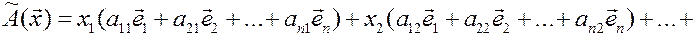
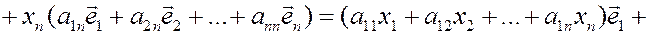
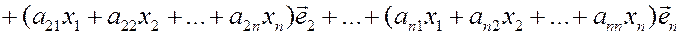С другой стороны, вектор 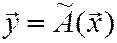, имеющий в том же базисе 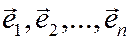координаты 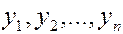, можно записать так:

.

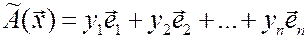В силу единственности разложения вектора по базису, имеем

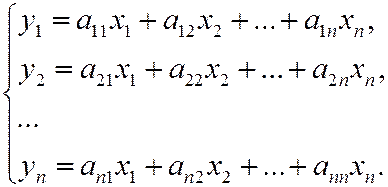
Матрица (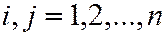) называется матрицей оператора 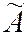в базисе 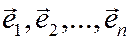, а ранг матрицы 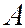- рангом оператора .

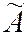Таким образом, имеем теорему.

Теорема 1. Каждому линейному оператору 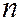-мерного пространства соответствует матрица 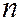-го порядка, и наоборот: всякой матрице 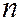-го порядка соответствует линейный оператор 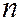-мерного пространства.

Связь между вектором и его образом 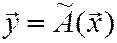можно выразить в матричной форме уравнением:

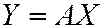, (1)

где 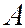- матрица линейного оператора, 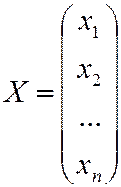и 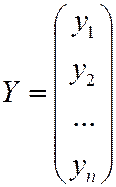- матрицы-столбцы из координат векторов и .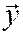

Пример 1. Пусть в пространстве 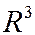линейный оператор 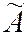в базисе 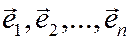задан матрицей 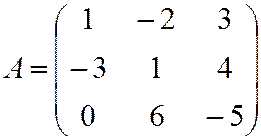. Найти образ 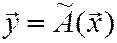вектора .

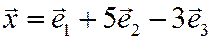Решение: По формуле (1)

.

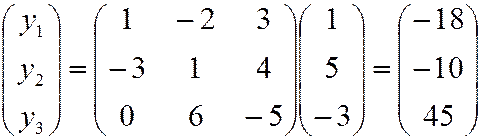Следовательно, .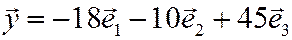

Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.

Теорема 2. Матрицы 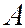и 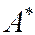линейного оператора 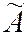в базисах 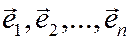и 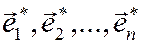связаны соотношением

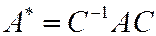, (2)

где 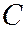- матрица перехода от старого базиса к новому.

Пример 2. Матрица 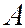линейного оператора 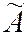задана в базисе 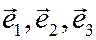: 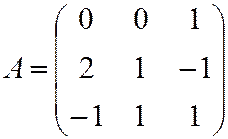. Найти ее в базисе , , .

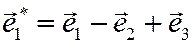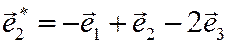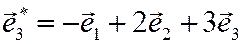Решение: По формуле (2) найдем матрицу перехода от старого к новому базису: .

Найдем .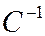

; ; ; ; ; ; ; ; ; .

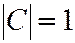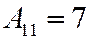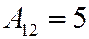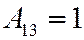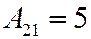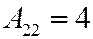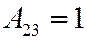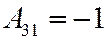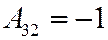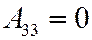Следовательно, .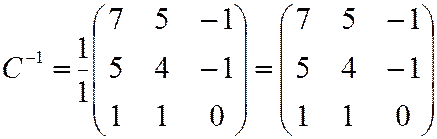

По формуле (2) найдем

.

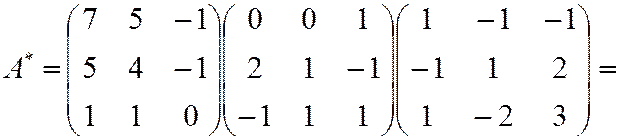
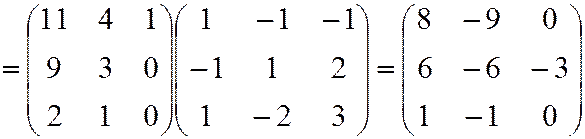Дата добавления: 2014-01-04