Типові ланки АСР та їхні передаточні функції

Типові ланки АСР. З'єднання ланок у системах.

Лекція № 13

1 Типові ланки АСР та їхні передаточні функції.

2 З'єднання ланок у системах.

Простейшая система автоматического регулирования со­стоит из двух основных элементов — объекта и регулятора. Динамические характеристики объекта принято составлять из простых звеньев, каждое из которых описывается простыми зависимостями. Соединяя прос­тейшие звенья в той или иной последовательности, можно по­лучить математическое описание объектов управления с лю­бой точностью.

Рассмотрим основные типовые линейные звенья: усилительное, инерционное, интегрирующее, реальное диф­ференцирующее и запаздывания.

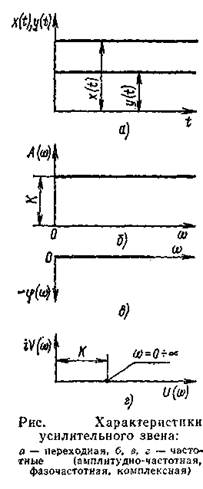
В усилительном звене зависимость между сигна­лами входа и выхода выражает­ся уравнением у(t)=K·x(t), (К — коэффициент усиления). Наибо­лее часто усилительные звенья встречаются в механических передачах и электрических це­пях. Переходная характеристи­ка усилительного звена пока­зана на рис. 3, а. Его пере­даточная функция определяется по формуле W(p)=K. Частотные характеристики звена (АЧХ, ФЧХ и КЧХ) показаны на рис. 3, б, в, г.

Свойства инерционного звена во временной области определяются зависимостью Ту'(t)+у(t)=Кх(t). Передаточная функция звена выражается уравнением W(p)=K/(Tp+1), где Т — постоянная времени (время, необходимое для измерения выходной величины от исходного значения до нового уста­новившегося значения при постоянной скорости, получен­ной в начальный момент); К — коэффициент пропорцио­нальности.

Переходная характеристика инерционного звена пока­зана на рис. 4, а, его амплитудно-частотная и фазочастотная характеристики — на рис. 4, б, в. Следует отметить что с увеличением частоты ФЧХ стремится к углу сдвигай π/2. Таким образом, в этом звене выходные частоты отстают от входных. Звенья, в которых выходные и входные коле­бания сдвинуты по фазе, называют фазосдвигающими.

Комплексную частотную характеристику инерционного звена определяют по формуле W(iω)=K/(Tiω+1). Графически она изображается в виде полуокружности в комп­лексной плоскости (рис. 4, г).

Свойствами интегрирующего звена обладают исполнительные механизмы с постоянной скоростью. Звено называют интегрирующим, если скорость изменение его выходной величины пропорциональна входной величине: у' (t)=K_иx(t), где К_и — коэффициент, имеющий раз­мерность, обратную времени.

На рис. 5, а показана переходная характеристика зве­на, передаточная функция которого W(p)=K_и/p. Комп­лексную частотную характеристику (КЧХ) звена определяют по формуле W(iω)=К_и/(iω).

Интегрирующее звено является также фазосдвигающим: φ(ω)=π/2. Частотные характеристики звена (ФЧХ, АЧХ, КЧХ) показаны на рис. 5, б, в, г.

Примером звена запаздывания может служить транспортер-дозатор сыпучих материалов. Входной сигнал, пройдя по транспортеру, проявится на выходи звена только через время τ; при этом он не претерпевает изменений по амплитуде. Временная (переходная) характеристика (рис. 6, а) звена имеет вид ступеньки, сдвинутой на время τ относительно момента возмущения. Таким образом, амплитудно-частотная характеристика представляет собой прямую, параллельную оси частот (рис. 6, б), при этом сдвиг по фазе линейно зависит от частоты: φ(ω) =2πτ/Т

Фазочастотная характеристика звена запаздывания гра­фически показана на рис. 6, в. Комплексная частотная характеристика звена, изображенная единичной окруж­ностью (рис. 6, г) с центром в начале координат, выражает­ся уравнением W(p)=exp( — iωτ). Из этого уравнения опре­деляют передаточную функцию звена W(p)=exp(—pτ).

В промышленности звенья запаздывания встречаются довольно часто (например, длинные трубопроводы, транс­портеры и другие участки объектов).

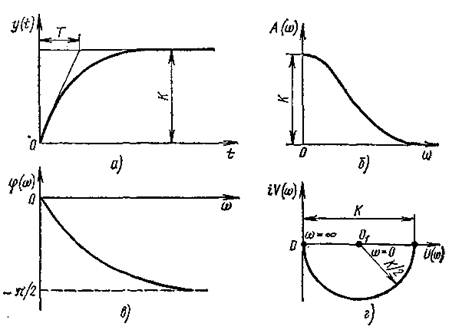
Рисунок 4 - Характеристики инерционного (апериодического) звена:

а — переходная, б, в, г — частотные (амплитудно-частотная, фазочастотная,

комплексная)

Рисунок 5 - Характеристики интегрирующего звена:

а—переходная, б, в, г — частотные (фазочастотная, амплитудно-

частотная, комплексная)

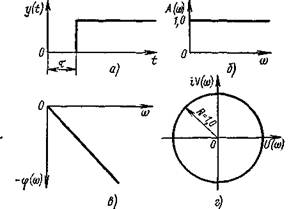
Рисунок 6 - Характеристики звена запаздывания:

а — переходная, б, в, г — частотные (амплитудно-частотная,

фазочастотная, комплексная)

Дата добавления: 2014-01-04