
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ІІ етап. Аналіз множини розв’язків СЛР
|
|
|
|
Якщо остання матриця І етапу містить нульовий рядок, якому відповідає ненульовий вільний член, то СЛР – несумісна, оскільки такий рядок відповідає рівнянню  . В протилежному випадку СЛР – сумісна.
. В протилежному випадку СЛР – сумісна.
Для сумісної СЛР: якщо вона містить вільні змінні, то система невизначена, інакше система визначена.
ІІІ етап. Зворотній хід методу (виконується лише для сумісних СЛР).
1. За останньою матрицею перетворень І етапу виписується відповідна СЛР (еквівалентна початковій за теоремою).
2. Надаючи вільним змінним (якщо такі є) довільних значень, їх переносять у праву частину кожного рівняння (матриця з базисних змінних стає верхньотрикутною, отже невиродженою).
3. Починаючи з останнього рівняння, знаходять відповідні значення базисних змінних.
4. Виписується розв’язок СЛР (у вигляді вектора).
Приклад 6. Розв’язати СЛР методом Гауса в залежності від параметра.
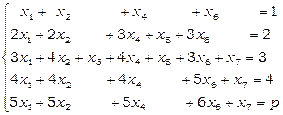
Випишемо розширену матрицю системи:
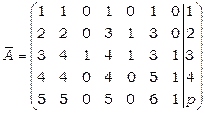 .
.
І етап складається з семи кроків, на кожному кроці ведучі елементи виділені у відповідній матриці.

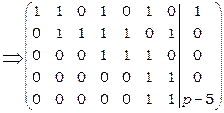 .
.
3-й крок: у третьому стовпчику останньої матриці, починаючи з відповідного місця (третього) немає ненульового елементу, отже 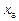 – вільна змінна.
– вільна змінна.
4-й крок: у четвертому стовпчику шукаємо ведучий, починаючи з третього місця (попередня змінна вільна).
 .
.
5-й крок: у п’ятому стовпчику останньої матриці, починаючи з відповідного місця (четвертого) немає ненульового елементу, отже  – вільна змінна.
– вільна змінна.
6-й крок: у шостому стовпчику шукаємо ведучий, починаючи з четвертого місця (попередня змінна вільна).
 .
.
7-й крок: у сьомому стовпчику останньої матриці, починаючи з відповідного місця (п’ятого) немає ненульового елементу, отже  – вільна змінна.
– вільна змінна.
І етап завершено, ненульові елементи матриці утворюють сходинки, матриця має східчастий вигляд.
ІІ етап. Виникає два можливих випадки.
1. Якщо  , то СЛР несумісна. Розв’язання закінчено.
, то СЛР несумісна. Розв’язання закінчено.
2. Якщо p =5, то СЛР сумісна та невизначена, оскільки є три вільні змінні. В цьому випадку з останньої матриці перетворень І етапу можна виключити останній рядок, оскільки він відповідає числовій тотожності 0=0. Тоді матриця набуває вигляду:
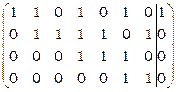
ІІІ етап (для p =5).
1. СЛР, що відповідає останній матриці, має вигляд:
 .
.
2. Надамо вільним змінним значень 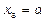 ,
,  ,
,  ,
,  , та перенесемо їх у праву частину кожного рівняння:
, та перенесемо їх у праву частину кожного рівняння:
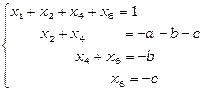
(матриця з базисних змінних – верхньотрикутна).
3. Знайдемо значення базисних змінних, починаючи з останнього рівняння:  .
.
4. Розв’язок СЛР  ,
,  .
.
Відповідь матиме вигляд: 1) якщо  , то СЛР несумісна;
, то СЛР несумісна;
2) якщо p =5, то СЛР сумісна та невизначена, будь-який її розв’язок задається вектором  ,
,  .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 492; Нарушение авторских прав?; Мы поможем в написании вашей работы!