Розвинення функцій у степеневі ряди. Ряд Тейлора

З’ясуємо, коли можна стверджувати, що задана функція є сума деякого степеневого ряду.

По-перше, сума степеневого ряду має нескінченну кількість похідних в інтервалі збіжності. Це необхідна умова того, що 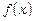є сума. Достатню з’ясуємо, коли побудуємо ряд для .

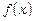Припустимо, що функція 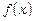має нескінчену кількість похідних в околі точки 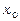і вона є сумою степеневого ряду в цьому околі:

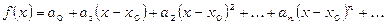. (14.34)

Коефіцієнти ряду 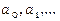залежать від функції 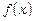. Вони невідомі, і треба їх визначити.

Візьмемо похідних від обох частин рівності (34):

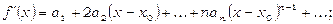
(14.35)

……………………………………………………………………..

.

Покладемо в рівностях (14.34) та (14.35) . Тоді визначимо коефіцієнти через значення функції 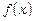та її похідних в точці 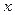, а саме:

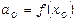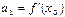, , , …, . (14.36)

Підставивши знайдені значення коефіцієнтів у формулу (14.34), отримаємо остаточно степеневий ряд, сумою якого є функція :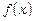

(14.37)

або в скороченому записі

. (14.38)

Ряд (14.37) або (14.38) називається рядом Тейлора для функції 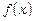. Частинний випадок, коли 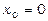, дає так званий ряд Маклорена:

або

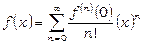. (14.39)

У записах через суму мається на увазі, що 0!=1.

Отримали розвинення функції 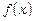у степеневий ряд, припустивши, що це можливо. Тепер повернемось до достатньої умови розвинення функції у степеневий ряд.

Нехай 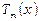- многочлен 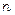-ого ступеня, який є 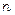-ою частинною сумою ряду Тейлора:

. (14.40)

Хоча коефіцієнти ряду Тейлора для функції 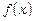визначені через значення функції 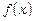та її похідних у точці 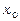, це ще не забезпечує збіжність ряду Тейлора саме до функції 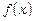. Якщо ряд Тейлора збігається до 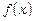, то, за визначенням, буде виконуватись рівність

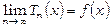
або

. (14.41)

Вираз 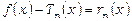- залишок ряду Тейлора для функції 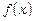. Таким чином, отримуємо достатню умову розвинення функції в ряд Тейлора: для того, щоб функція 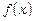при деякому значенні була сумою степеневого ряду, необхідно, щоб вона була диференційована нескінченну кількість разів, і достатньо, щоб залишок ряду Тейлора прямував до нуля при 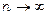при цьому значенні 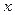, тобто щоб справджувалась рівність

. (14.42)

При дослідженні залишку ряду користуються його виразом у формі Лагранжа:

, (14.43)

а також виразом залишку у формі Коші:

, (14.44)

де 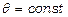- правильний додатний дріб:

. (14.45)

Практично при розвиненні функції у степеневий ряд беруть конкретне число членів, щоб витримати точність обчислення. Залишок 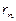дає помилку, яка виникає при заміні функції многочленом Тейлора .

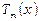Зауваження. Якщо в околі точки 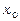функція 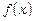може бути розвинена у степеневий ряд, то останній може бути тільки рядом Тейлора.

Коефіцієнти степеневого ряду (14.34) визначаються однозначно, вони є коефіцієнтами Тейлора (14.36).

Приклад 16. Розвинути у степеневий ряд функцію в околі точки .

Знайдемо 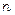похідних заданої функції:

; ; ; ; ;.; ;….

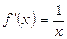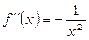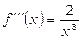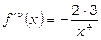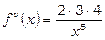Обчислимо коефіцієнти Тейлора в точці :

, , ;

, ;

, …;

, ….

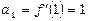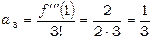Підставимо ці значення у ряд (14.34):

, .

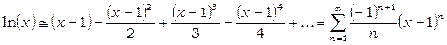Дата добавления: 2014-01-04