Нормальний закон розподілу і його особливості

Основні закони розподілу випадкових величин.

Нормальний розподіл - найбільше що часто зустрічається вид розподілу. З ним доводиться зіштовхуватися при аналізі погрішностей вимірів, контролі технологічних процесів і режимів, а також при аналізі й прогнозуванні різних явищ в економіці, соціології, демографії й інших областях знань.

Найбільш важливою умовою виникнення нормального розподілу є формування ознаки як суми великого числа взаємно незалежних що складаються, жодне з яких не характеризується винятково великий у порівнянні з іншими дисперсією. У виробничих умовах такі передумови в основному дотримуються.

Головна особливість нормального розподілу полягає в тому, що воно є граничним, до якого наближаються інші розподіли.

Нормальним називається розподіл, функція щільності ймовірності якого має вигляд

,

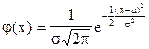де (- математичне очікування випадкової величини;

s² - дисперсія випадкової величини, характеристика розсіювання значень випадкової величини біля математичного очікування.

Розподіл Пирсона (c² - хи квадрат)

Якщо X₁, X₂,..., X_n є ряд незалежних, нормованих, нормально розподілених випадкових величин N(0,1), тобто MX_i=0 і Dx_i=1 для i=1, 2,..., (, те випадкова величина

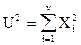(2.3)

має розподіл c² з n ступенями волі, де n - єдиний параметр розподілу c², що характеризує число незалежних випадкових величин у вираженні (2.3).

У таблицях додатка для різних n приводяться числа, імовірність перевищення яких випадковою величиною U² дорівнює заданому значенню рівня значимості a=1-g.

Відзначимо, що математичне очікування випадкової величини U² дорівнює числу ступенів волі n, а дисперсія - подвоєному числу ступенів волі

MU²=n; DU²=2n (2.4)

Розподіл Пирсона використовується для побудови довірчого інтервалу для генеральної дисперсії s².

Розподіл Стьюдента (t - розподіл)

Був розглянутий закон розподілу середньої арифметичної 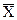, залежної від середнього квадратичного відхилення s генеральної сукупності. Однак у багатьох практичних додатках математичної статистики параметр s, як правило, не відомий. У цьому зв'язку виникає задача визначення закону розподілу 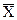, що не залежить від s, що вирішив англійський статистик Госсет, що публікувався під псевдонімом Стьюдент. Розподіл Стьюдента знаходить широке застосування в теорії статистичного оцінювання параметрів генеральної сукупності й у перевірці статистичних гіпотез.

Дамо визначення випадкової величини, що має розподіл Стьюдента.

Якщо випадкова величина Z має нормований розподіл N(0;1), а величина U² має розподіл c² з n ступенями волі, причому Z і U взаємно незалежні, то випадкова величина

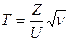
має t розподіл з 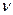ступенями волі.

Найбільше застосування на практиці знаходять таблиці, у яких дані значення t(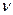,(), що відповідають заданому числу ступенів волі 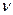=1, 2,..., і рівню значимості (, тобто ймовірності виконання нерівності P[(T(>t(,()]=.

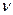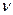Якщо з генеральної сукупності X з нормальним законом розподілу N((;() узята випадкова вибірка об'ємом n, то статистика

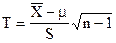
має розподіл Стьюдента з 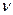=n-1 ступенями волі.

Розподіл Стьюдента (t - розподіл) використовується при інтервальний оцінці математичного очікування при невідомому значенні середнього квадратичного відхилення .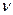

Теорія статистичного оцінювання розглядає два основних види оцінок параметрів розподілів: крапкові й інтервальні оцінки.

Дата добавления: 2014-01-04