Однорідні СЛАР

Означення. Система називається однорідною якщо всі її вільні члени рівні нулю, інакше – система називається неоднорідною. (Однорідна, коли всі доданки однакового степеня.)

Однорідна система має завжди хоча б один розв’язок – нульовий (0;0;…0).

Нехай однорідна система квадратна. Якщо 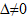- один розв’язок (тільки нульовий).

Якщо 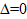- розв’язків безліч.

Властивості розв’язків однорідної системи.
1) якщо 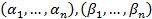- розв’язки системи,

то і їх сума - теж розв’язок.

2) якщо- розв’язок системи, k- будь-яке число, то - теж розв’язок.

Вправа. Довести.

Означення. Якщо для деякої множини об’єктів V виконуються такі властивості:

x є V, y є V=> x + y є V; x є V, k є ℝ => kx є V (замкнутість множини V відносно додавання та множення на число). Також виконуються властивості:
перестановочна (комутативність): x+y=y+x;
розподільча (асоціативність): (x + y) + z = x + (y + z);

існує єдиний нульовий елемент 0 є V, такий що 0+х=х для будь-якого х є V;

для кожного елемента х є V існує єдиний протилежний вектор –х, такий що х+(-х)=0;

1×х=х; (km)x=k(mx)

дистрибутивна: k(x + y) = kx +ky, (k+m)x=kx+mx (x,y,z є V, k, m є ℝ).

Тоді множина V- називається лінійним простором (над полем дійсних чисел).

Отже, множина розв’язків однорідної СЛАР є лінійним простором.

Означення. Базис (синонім – основа).

Базисом чи фундаментальною сукупністю елементів лінійного простору V - називається така сукупність його об’єктів через які о д н о з н а ч н о можна виразити будь-який об’єкт лінійного простору з допомогою дій додавання та множення на число.

Вправа. Довести, що елементи базису лінійно незалежні. (Тому що нульовий елемент теж повинен отримуватися єдиним способом, тобто тільки коли всі коефіцієнти .

Вправа.* Довести що в будь якому базисі простору V є однакова кількість елементів.

Означення. Кількість елементів у базисі називається розмірністю простору.

Приклад (одновимірного простору). (2,4,5) – рядок базис. Лінійний простір

V= {(2z;4z;5z), z є ℝ} буде одновимірним.

Базис розв’язків однорідної системи частіше називають фундаментальною системою розв’язків цієї системи.

Приклад 1. Знайти всі розв’язки і фундаментальну систему розв’язків однорідної системи

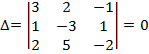
теж рівні 0 (бо є нульовий стовпчик). Буде безліч розв’язків. Пошукаємо залежне рівняння:

Можна викреслити третє рівняння.

=>

;

;

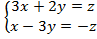
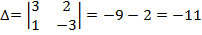
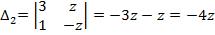
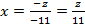– простір розв’язків.

Пошукаємо фундаментальну систему розв’язків. .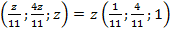

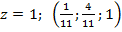– фундаментальна система розв’язків (ФСР), тому що всі інші розв’язки можна отримати з цього одного єдиним способом, помноживши його на відповідне число z. (Простір розв’язків – одновимірний).

Відповідь. — ФСР.

Приклад 2.

,

.

.

=

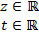
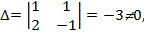
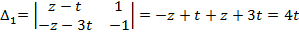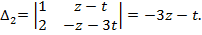
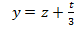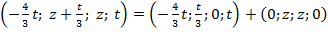Отже, ФСР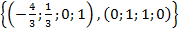

Відповідь. 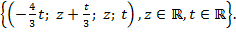ФСР: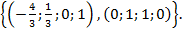

Тепер очевидним є алгоритм знаходження ФСР коли відомий загальний розв’язок однорідної системи: Нехай є деяка кількість вільних невідомих t,z,s,…,p. Потрібно надати їм таких значень t=1, z=0,s=0,…,p=0; t=0, z=1,s=0,…,p=0; … t=0, z=0,s=0,…,p=1.

Тоді отримані розв’язки складуть ФСР (бо через них можна виразити будь-який розв’язок системи однозначно).

Отже, кількість вільних невідомих буде розмірністю простору розв’язків однорідної системи.

Теорема (про розв’язок неоднорідної системи і відповідної однорідної).

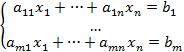
Відповідна однорідна система це система, в якої вільні члени замінено на нулі:

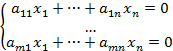
Щоб отримати всі розв’язки неоднорідної системи (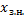– загальний розв’язок неоднорідної системи), треба знати один її частковий розв’язок () і всі розв’язки відповідної однорідної системи (– загальний розв’язок однорідної). Тоді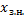

Доведення. Випливає з двох очевидних властивостей: 1) різниця двох розв’язків неоднорідної системи є розв’язком відповідної однорідної системи; 2) якщо до розв’язку неоднорідної системи додати розв’язок відповідної однорідної, отримаємо розв’язок неоднорідної системи.

Дата добавления: 2014-01-04