
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения. 1. Проверить, что, s s+1x =s x, s s+2x =s 2x, s -1x = s s-1x, , s(О(x))=О(х), s k(О(х)) = О(x), О(sx) =О(х)
|
|
|
|
1. Проверить, что, s s+1x =s x, s s+2x =s 2x, s -1x = s s-1x, …, s(О(x))=О(х), s k(О(х)) = О(x), О(sx) =О(х), О(s kх) = О(x), О(х) = {s kx| k =0,1, 2,…, s-1 } = {s kx| k Î Z }.
2. Проверить, что циклы разных элементов либо не пересекаются, либо совпадают.
Таким образом, множество Х разбивается в объединение непересекающихся циклов.
Пусть х = a1, s x = a2 , s 2x = a3 , s 3x = a4 ,…, s s-1x = as, и соответственно цикл О(х) ={a1, a2 ,.., as}. Тогда s(О(x))= О(х), и s на О(x) является биекцией, которую можно записать в виде таблицы  или в виде таблицы с одной строкой: (a1, a2, a3,…, as). Запись s в виде такой строки означает, что s a1= a2, s a2= a3 ,…,s as-1= as, s as= a1 . Записывая подстановку на каждом цикле в виде одной строки, получим циклическую запись подстановки. Так, например, подстановка
или в виде таблицы с одной строкой: (a1, a2, a3,…, as). Запись s в виде такой строки означает, что s a1= a2, s a2= a3 ,…,s as-1= as, s as= a1 . Записывая подстановку на каждом цикле в виде одной строки, получим циклическую запись подстановки. Так, например, подстановка
s = 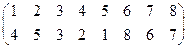 в циклической записи имеет вид s =(1, 4, 2, 5)(3)(6, 8, 7).
в циклической записи имеет вид s =(1, 4, 2, 5)(3)(6, 8, 7).
Определение. Транспозицией будем называть подстановку tij такую, что tij (i)= j, tij (j) = i, tij (k) = k при k ¹ i, k¹j.
Очевидно, tij-1 = tij, tij2 = tij.
Утверждение. Любую подстановку s Î Sn, п ³ 2, можно разложить в композицию транспозиций.
Доказательство по индукции.
1. При п =2 утверждение очевидно, так как S2 состоит из двух элементов: id и tij.
2. Пусть для п – 1 утверждение верно. Рассмотрим s Î Sn. Пусть s(п) = q, и s1 = tqn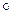 s. Тогда s1 (n) = n, и s1 – биекция множества {1, 2, 3, …, n -1 } из (п-1)- го элемента. По предположению индукции можно считать, что для s1 утверждение верно, то есть s1=t1
s. Тогда s1 (n) = n, и s1 – биекция множества {1, 2, 3, …, n -1 } из (п-1)- го элемента. По предположению индукции можно считать, что для s1 утверждение верно, то есть s1=t1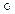 t2
t2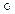 …
…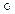 tr - композиция транспозиций. Но s = tqn-1
tr - композиция транспозиций. Но s = tqn-1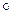 s1 = tqn
s1 = tqn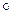 s1 = tqn
s1 = tqn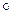 t1
t1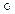 t2
t2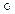 …
…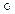 tr - композиция транспозиций.
tr - композиция транспозиций.
Очевидно, разложение подстановки в композицию транспозиций неоднозначно.
На практике очень легко раскладывать подстановку в произведение транспозиций, если она задана в циклической записи. Так, например, легко проверить, что
(1, 3, 7, 2, 4)(5, 6)(8) = t13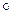 t37
t37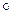 t72
t72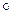 t24
t24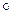 t56.
t56.
Будем говорить, что в последовательности чисел i1, i2 ,..,in два числа ik и il образуют инверсию, если ik > il, но ik расположено левее il. Подстановка s =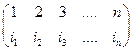 называется четной, если количество инверсий в её нижней строке
называется четной, если количество инверсий в её нижней строке
четно, и s называется нечетной, если количество инверсий в
её нижней строке нечетно.
Утверждение. Если количество инверсий в нижней строке подстановки s равно m, то s можно разложить в произведение m транспозиций.
Доказательство. Пусть два соседних элемента ik и ik+1 в нижней строке подстановки s образуют инверсию. Тогда
s1=
 s =
s = , и число инверсий в нижней строке у s1 равно m – 1. Продолжая эту процедуру далее, получим, что существуют транспозиции t1 ,t2 , …,tm такие, что подстановка tm
, и число инверсий в нижней строке у s1 равно m – 1. Продолжая эту процедуру далее, получим, что существуют транспозиции t1 ,t2 , …,tm такие, что подстановка tm tm-1
tm-1 …
… t1
t1 s не имеет инверсий в нижней строке, то есть tm
s не имеет инверсий в нижней строке, то есть tm tm-1
tm-1 …
… t1
t1 s = id. Умножая последнее равенство слева на tm, затем на tm-1 и так далее до t1, и учитывая, что все ti2= id, получим, что s = t1
s = id. Умножая последнее равенство слева на tm, затем на tm-1 и так далее до t1, и учитывая, что все ti2= id, получим, что s = t1 t2
t2 …
… tm.
tm.
Лекция 4.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 248; Нарушение авторских прав?; Мы поможем в написании вашей работы!