Определения. Пусть P – некоторое поле

Пусть P – некоторое поле.

Системой m линейных уравнений с п неизвестными называется система уравнений вида:

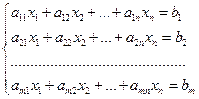, (4.1)

где все a_ij, b_i Î P.

Для простоты такую систему мы будем записывать таблицей вида:

Такая таблица 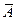называется расширенной матрицей системы линейных уравнений. Матрица

A =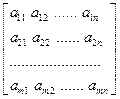

называется основной матрицей системы. Сокращенно систему линейных уравнений будем называть СЛУ. Очевидно, по расширенной матрице СЛУ восстанавливается однозначно.

Решением системы линейных уравнений называется такой набор (с₁, …,с_n) элементов из P, что при подстановке в систему х₁ = с₁, …, х_п = с_n получаются верные равенства:

a₁₁ с₁ + … + a_1n с_n = b₁, a₂₁ с₁ + … + a_2n с_n = b₂, …

Если у системы имеются решения, то она называется совместной. Если у системы нет решений, то она называется несовместной. Если у системы имеется единственное решение (с₁, …,с_n), то она называется определенной. Если у системы имеется более одного решения, то она называется неопределенной.

Определим для строчек с элементами из поля Р операции так: (a₁, …, a_n)+ (b₁, …,b_n) = (a₁ + b₁, …, a_n + b_n) – сложение строчек, и с×(a₁, …,a_n)= (сa₁, …,сa_n) – умножение строчки на элемент сÎ Р.

Такие операции мы будем проделывать со строчками расширенной матрицы СЛУ. Очевидно, сумме строчек расширенной матрицы соответствует сумма соответствующих уравнений системы, а умножению строчки на элемент сÎ Р соответствует умножение соответствующего уравнения на с.

Будем говорить, что система S¢ является следствием системы S, если любое решение системы S является решением системы S¢. Обозначать этот факт будем так: S Þ S¢. Будем говорить, что системы S и S¢ равносильны, если S Þ S¢ и S¢ Þ S. Записывать это будем так: S Û S¢. Другими словами, S Û S¢ тогда и только тогда, когда множества решений систем S и S¢ совпадают.

Утверждение. Отношение равносильности Û на множестве систем линейных уравнений с п неизвестными является отношением эквивалентности.

Доказательство очевидно.

Следовательно, множество систем линейных уравнений разбивается на классы эквивалентных. Для решения произвольной СЛУ было бы удобно найти в классе эквивалентных ей систем наиболее простую систему и найти все решения этой наиболее простой системы. Это множество решений будет совпадать с множеством решений первоначальной СЛУ. Далее мы и будем искать наиболее простые системы среди систем, эквивалентных данной.

Дата добавления: 2014-01-04