
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обчислення середніх значень економічних функцій
|
|
|
|
.
Застосування в динамічних процесах
Економічні застосування
1. Розглянемо задачу про обсяг продукції.
Нехай деяке підприємство (фірма) виробляє продукцію з інтенсивністю (продуктивністю праці) f = f (t). Знайдемо обсяг продукції q, виробленої за інтервал часу [0; T].
Очевидно, що інтенсивність виробництва продукції не змінюється (f = f (t) = const), то обсяг продукції q, виробленої за інтервал часу [0; T], обчислюється за формулою q = f T.
Визначений інтеграл  чисельно дорівнює обсягу виробленої продукції підприємством (фірмою) з продуктивністю праці f = f (t) за інтервал часу [0; T].
чисельно дорівнює обсягу виробленої продукції підприємством (фірмою) з продуктивністю праці f = f (t) за інтервал часу [0; T].
2. В економічній теорії виробнича функція Кобба-Дугласа, яка враховує технічний прогрес, має вигляд
 ,
,
де К – обсяг фондів; L – обсяг трудових ресурсів; λ – інтенсивність розвитку виробництва, пов’язаного з технічним прогресом. Тоді, згідно з економічним змістом виробничої функції Кобба-Дугласа можна показати, що обсяг виробленої за Т років продукції визначається за формулою  . (1)
. (1)
Приклад. Знайдемо обсяг продукції, виробленої фірмою за два роки, якщо виробнича функція Кобба-Дугласа має вигляд f (t) = (1 + 2 t) ∙ e 5 t.
Розв’язання. За формулою (1) дістанемо

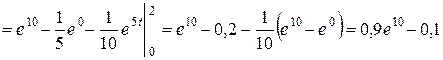 .
.
В економічних задачах часто використовують теорему про середнє значення, яку ви розглядали, коли вивчали властивості визначених інтегралів.
Якщо С = С (t), R = R (t), P = P (t) – відповідно змінні витрати, доход прибуток підприємства (фірми), то їхні середні значення за час від t = t0 до t = t1 обчислюються за формулами:
 , (2)
, (2)
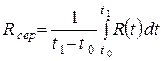 , (3)
, (3)
 (4)
(4)
відповідно.
Приклад. Знайти середній доход зо 10 міс. поточного року, якщо задано функцію доходу фірми 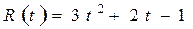 , де t – час.
, де t – час.
Розв’язання. За умовою середній доход фірми потрібно визначити за інтервал часу від 0 до 10. використовуємо формулу (3), маємо
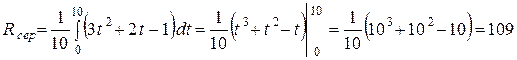 .
.
Раніше ми розглядали різні граничні функції (граничний доход, граничні витрати, граничний прибуток). Також було показано, що граничні функції можна дістати з відповідних економічних функцій диференціюванням. Інтегрування дає змогу розв’язати обернену задачу: знайти дану економічну функцію за відповідною граничною функцією.
Якщо C ′ (x), R ′ (x), P ′ (x) - відповідно функції граничних витрат, доходу та прибутку підприємства (фірми), то при реалізації х одиниць товару (продукції) зміни витрат, доходу й прибутку зі збільшенням реалізації виробленої продукції від a до b одиниць обчислюються за формулами
 ; (5)
; (5)
 ; (6)
; (6)
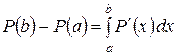 . (7)
. (7)
Якщо витрати на виготовлення одиниці продукції зростають за законом y = f (x), то фактичне зв’язування обігових коштів при цьому обчислюється за формулою
 (8)
(8)
Умовне зв’язування обігових коштів (якщо всі витрати виплатити в перший день) Cyмов = t ∙ C, де t – тривалість циклу виробництва, а С – загальні витрати.
Коефіцієнт готовності одиниці продукції обчислюється за формулою
 (9)
(9)
Приклад. Задано граничний прибуток фірми Р ′ (х) = 23,5-0,01х. Визначити зростання прибутку, якщо реалізація продукції збільшується з 1000 до 1500 одиниць.
Розв’язання. Зростання прибутку фірми знайдемо за формулою (7):
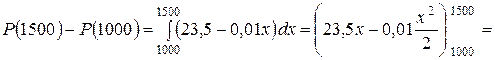
 .
.
Відповідь Прибуток зросте на 5500 ум. од.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1780; Нарушение авторских прав?; Мы поможем в написании вашей работы!