Розв’язати рівняння з параметрами — означає знайти всі розв’язки цього рівняння для кожної допустимої системи значень параметрів

Щоб розв’язати рівняння (1), потрібно:

1) визначити область допустимих значень параметрів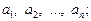

2) розв’язати рівняння (1) відносно х і подати невідоме х у вигляді функції 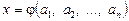від параметрів;

3) з’ясувати, при яких допустимих значеннях параметрів значення функції 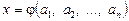є розв’язками даного рівняння;

4) розглянути рівняння (1) при таких допустимих значеннях параметрів, при яких його не можна розв’язати відносно х і з’ясу­вати чи має рівняння при цих значеннях параметрів розв’язки і, якщо має, то які.

Основні види рівнянь з параметрами які зустрічаються на вступних іспитах можна розбити на такі класи:

1. Лінійні рівняння з параметром.

2. Дробові — раціональні рівняння з параметром.

3. Квадратні рівняння з параметром.

4. Ірраціональні рівняння з параметрами.

До найпоширеніших методів розв’язання рівнянь з параметром відноситься графічний метод.

Цей вид рівнянь достатньо висвітлено в літературі [4—7].

У цьому посібнику не має змоги розглянути всю інформацію по задачам з параметрами, тому спинимось на двох видах рівнянь:

1. Лінійне рівняння та системи рівнянь з параметрами.

2. Квадратні рівняння з параметрами.

Серед методів розглянемо застосування графічного методу до розв’язування деяких задач.

12.1. Лінійні рівняння з параметром

Означення. Рівняння виду

(1)

де х — невідоме; 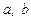— параметри, називають лінійним рівнянням з параметрами.

Дослідимо рівняння (1).

1. Якщо , то рівняння (1) має єдиний розв’язок: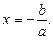

2. Якщо 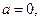, то рівняння (1) має безліч розв’язків.

3. Якщо 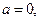то рівняння не має розв’язків.

Приклад. При якому значенні параметра b рівняння має безліч розв’язків?

Ø Використовуючи схему дослідження лінійного рівняння, маємо:

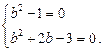
Розв’язуючи цю систему, дістаємо:

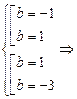отже,

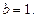
Відповідь. При 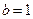система рівнянь має безліч розв’язків.

Приклад. При якому значенні параметра b рівняння

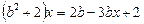
не має розв’язку?

Ø Після перетворення рівняння до виду

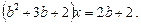
Останнє рівняння не має розв’язків якщо

,

звідки

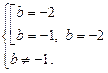
Відповідь. .

Приклад. При яких значеннях с рівняння 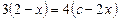має додатні розв’язки?

Ø Спочатку зводимо рівняння до загального виду. Дістанемо,

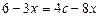
або

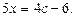
За умовою задачі тому 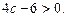Отже

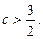
Відповідь.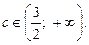

Приклад. Визначити, при яких значеннях параметра а корені рівняння кратні 3.

Ø Зводячи рівняння до вигляду

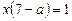
дістанемо єдиний розв’язок при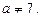

За умовою корені рівняння кратні 3, тобто де Звідси

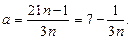
Відповідь.

1. При якому значення параметра в рівняння має безліч розв’язків? ().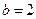

2. При якому значення параметра з рівняння 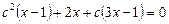має безліч розв’язків? ().

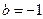3. При якому значенні параметра а рівняння 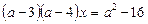не має розв’язку? ().

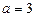4. Визначити при яких значеннях рівняння має додатні розв’язки. ().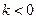

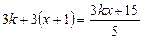5. При якому значенні параметрів рівняння не має розв’язку? ().

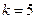6. Визначити при яких значеннях параметра а корені рівняння 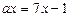кратні 5. ().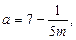

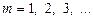7. Розв’язати рівняння

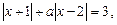
де а — параметр.

(Якщо 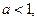то ;

то ;

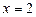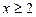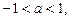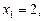
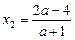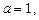то ;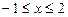

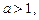то ;

то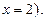

8. При яких значеннях параметра а всі розв’язки рівняння 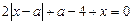задовольняє нерівність ?

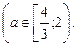
9. При яких значеннях параметра а рівняння має не менше чотирьох цілих коренів?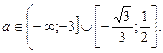

10. При яких значеннях параметра а рівняння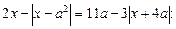

а) не має розв’язків;

б) має скінченну множину розв’язків?

12.2. Квадратні рівняння з параметром

Рівняння виду де 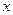— шукане невідоме, 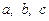— параметри, називається квадратним рівнянням з параметрами.

Корені квадратного рівняння знаходимо за формулою:

, де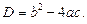

1. Якщо 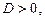то рівняння має 2 дійсні корені.

2. Якщо 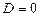, то рівняння має єдиний корінь.

3. Якщо 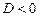, то рівняння не має дійсних коренів.

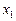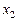Для коренів і квадратного рівняння виконуються наступні теореми.

Розглянемо деякі властивості квадратного тричлена. Виділяючи повний квадрат, дістаємо формулу:

,

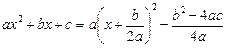із якої маємо, що графік квадратичної функції дістаємо з графіка функції за допомогою двох паралельних перенесень — зсуву на величину вздовж осі Ох і зсуву на величину 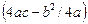вздовж осі Оу.

Тому координати визначаються параметром

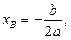
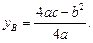
Віссю симетрії параболи є пряма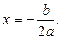

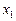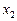Теорема (Вієта). Між коренями і квадратного рівняння існують співвідношення:

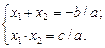
Зауваження. Дуже часто теорема Вієта провокує учнів
на відгадування коренів рівняння (усне розв’язування) замість його розв’язування за формулою коренів квадратного рівняння. Але можна 10 разів усно правильно знайти корені квадратного рівняння за теоремою, але на 11 раз помилитися. Уявіть собі, що цей 11 раз відбудеться на іспиті?! Що може бути гіршим за помилку при обчисленні на письмовому іспиті?

Незважуючи на попереднє зауваження, теорема Вієта може успішно застосовуватися при розв’язуванні різних задач, зокрема, задач на дослідження знаків коренів квадратичного рівняння. Це надійний інструмент для розв’язування багатьох задач з параметрами для квадратичної функції.

Теорема. Для того щоб корені квадратного рівняння мали однакові знаки, необхідно і достатньо, щоб виконувалися співвідношеня:

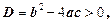
Дата добавления: 2014-01-04