Основні означення. Повернемось ще раз до питання оцінювання невідомих параметрів розподілу за вибірковими даними

Повернемось ще раз до питання оцінювання невідомих параметрів розподілу за вибірковими даними. Оскільки при оцінюванні параметра одним числом 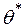ми отримуємо певне наближення до його істинного значення 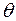, то отриманий результат не обов’язково буде співпадати з відповідним параметром генеральної сукупності. Виникає необхідність визначити точність, з якою здійснюється оцінювання, і його надійність. Тобто необхідно знати, до яких помилок може призвести заміна параметру 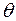його точковою оцінкою 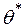і з якою впевненістю можна стверджувати, що ці помилки не виходять за означені межі. Це особливо актуально для аналізу малих вибіркових сукупностей. Відповіддю на ці питання є побудова довірчого інтервалу, до якого із заздалегідь визначеною надійністю належатиме значення параметра 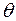, що оцінюється.

Нехай незалежна вибіркова сукупність 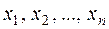є репрезентативним відображенням розподілу, що залежить від парамет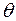ра (). Довірчим інтервалом параметра 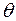називається інтервал, до якого параметр, що оцінюється, належить з ймовірністю, яка не менша за довірчу ймовірність (надійністьоцінки ):

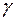, (12.1)

де – нижня границя довірчого інтервалу;

– верхня границя довірчого інтервалу.

Зверніть увагу, що значення границь довірчого інтервалу є функціями від значень варіант у вибірковій сукупності.

Отже, довірчий інтервал покриває параметр 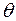, що підлягає оцінюванню, з надійністю .

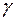Оскільки довірчий інтервал є симетричним відносно точкової оцінки то вимога (12.1) може бути записана у вигляді:

, (12.2)

де 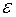– гранична похибка оцінки.

Зазвичай, значення довірчої ймовірності обумовлюється заздалегідь і відповідно з цим значенням обчислюються границі довірчого інтервалу, тому довірчий інтервал також має назву 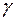– довірчий інтервал.

Слід зазначити, що в тому випадку, коли генеральну сукупність утворюють значення випадкової величини (певної ознаки), що має кількісне надання, то довірчий інтервал будують для цієї ознаки. Якщо ознака має тільки якісне надання, тобто не вимірюється у сильних шкалах, то довірчий інтервал, як правило, будують для ймовірностей.

Загально прийнятими є два рівні довірчої ймовірності: 0,95 та 0,99. Якщо мова йде про надійність оцінки, то цю величину прийнято визначати у відсотках: 95% та 99%. Існують і інші рівні надійності. Вибір того чи іншого значення довірчої ймовірності визначається дослідником залежно від міри відповідальності дослідження.

Зрозуміло, що існує і зворотна задача: визначення надійності, з якою невідомий параметр розподілу належатиме інтервалу, довжина якого вибрана заздалегідь.

Поряд з надійністю оцінки 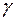розглядається рівень значущості 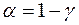. Він визначає ймовірність того, що при заданому рівні надійності значення параметру 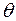, який оцінюється за вибірковою сукупністю, вийде за межі довірчого інтервалу. Наприклад, якщо за результатами статистичного оцінювання побудовано довірчий інтервал для цього параметру з надійністю 95%, то значення параметра у генеральній сукупності може вийти за межі довірчого інтервалу не більше, ніж у п’яти випадках із ста.

Дата добавления: 2014-01-04