Динаміка спеціальної теорії відносності

Релятивістський імпульс. Нехай у деякій інерціальній К–системі відліку назустріч одна одній рухаються дві однакові частинки 1 і 2 з однаковою швидкістю v₀, але під кутом a до вісі X. У цій системі відліку сумарний імпульс обох частинок зберігається: до і після зіткнення він дорівнює нулю. З'ясуємо, як буде обстояти справа в інший інерціальній системі відліку. Нехай СВ 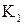рухається вправо зі швидкістю 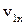, а СВ К₂ рухається вліво зі швидкістю 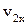. Розглянемо зіткнення в 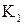–системі, де частинка 1 має швидкість u. Знайдемо У–складову швидкості частинки 2 у цій системі відліку, позначивши її 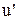. Ця частинка рухається зі швидкістю u уздовж вісі Y у К_2–системи і, крім того, разом з К₂–системою переміщується вліво зі швидкістю V відносно 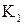–системи. За законом додавання швидкостей 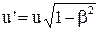. Закон збереження імпульсу в проекціях на вісь У має вигляд: 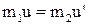. Після підстановки одержуємо: 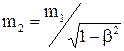. Якщо 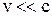, то b²®0 і – маса спокою, що є інваріантною величиною, тобто однаковою у всіх системах відліку. Саме маса 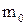є характеристикою частинки. Тоді маса, що визначається з вираження 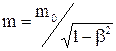, називається релятивістською масою, яка залежить від швидкості руху частинки. З урахуванням поняття релятивістської маси формула релятивістського імпульсу частинки здобуває вигляд:

.

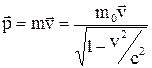Основне рівняння релятивістської динаміки.

Нехай під дією рівнодіючої зовнішньої сили 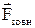імпульс частинки змінився на 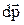. Тоді відповідно до основного рівняння динаміки можна записати: . Підставивши формулу релятивістського імпульсу в останню формулу, одержуємо:

.

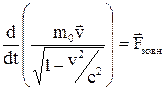Отримане рівняння є основним рівнянням релятивістської динаміки. Воно дозволяє знайти закон діючої на частинку сили F, якщо відома залежність від часу релятивістського імпульсу p(t), а з іншого боку, знайти рівняння руху частинки r(t), якщо відомі діюча сила і початкові умови – швидкість v₀ і положення r₀ частинки в початковий момент часу.

Кінетична енергія релятивістської частинки.

Визначимо кінетичну енергію як величину, збільшення якої дорівнює роботі діючої на частинку сили. Нехай вектора сили і швидкості за напрямком збігаються. Збільшення кінетичної енергії частинки dК під дією сили F на елементарному шляху dr=vdt дорівнює 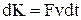. Відповідно до основного рівняння релятивістської динаміки 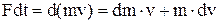, де m – релятивістська маса. Тому:

.

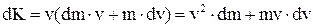Отримане вираження можна спростити, використовуючи формулу релятивістської маси. Зведемо цю формулу в квадрат і приведемо її до вигляду:

.

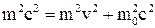Знайдемо диференціал цього вираження, маючи на увазі, що 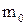і с – сталі величини: 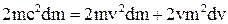. Розділимо отримане рівняння на 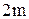: 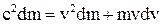. Після підстановки останнього вираження у формулу кінетичної енергії одержуємо: 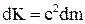. Таким чином, збільшення кінетичної енергії частинки пропорційне збільшенню її релятивістської маси. Кінетична енергія частинки, що знаходиться у стані спокою, дорівнює нулю, а її релятивістська маса 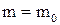. Проінтегрувавши формулу збільшення кінетичної енергії, одержимо:

или .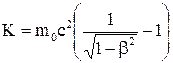

Останнє вираження називається формулою релятивістської кінетичної енергії.

Закон взаємозв'язку маси й енергії.

Перепишемо вираження для релятивістської кінетичної енергії у вигляді:

.

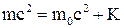Глибокий аналіз останньої формули привів Ейнштейна до наступних висновків:

- якщо тіло внаслідок свого існування має масу спокою 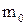, то воно має енергію спокою ;

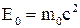- повна енергія тіла визначається з вираження: 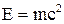. Вона дорівнює сумі енергії спокою і кінетичної енергії тіла: .

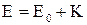Отримане співвідношення називається законом взаємозв'язку маси і енергії. З закону випливає, що маса тіла є мірою енерговмістимості тіла. Зміна енергії спокою тіла супроводжується еквівалентною зміною його маси:

.

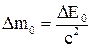Дата добавления: 2014-01-04