Критерії згоди щодо закону розподілу

Часто закон розподілу випадкової величини в генеральній сукупності є невідомим, але певні припущення відносно його характеру можна зробити, судячи з гістограми у вибірковій сукупності. У цьому випадку перевіряють гіпотезу щодо закону розподілу у генеральній сукупності. Основна гіпотеза у цьому випадку полягає у тому, що розбіжність між емпіричними частотами і частотами, що обчислюються відповідно до певного закону розподілу, є статистично не значущою. Для перевірки цієї гіпотези можуть застосовуватись кілька критеріїв згоди.

13.6.1. Критерій згоди Пірсона. Для перевірки основної гіпотези щодо закону розподілу в генеральній сукупності обчислюється випадкова величина:

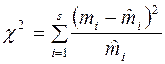, (13.7)

де 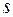– кількість інтервалів згрупованого ряду розподілу;

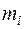– емпіричні частоти, тобто ті, що спостерігаються у вибірковій сукупності;

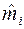– теоретичні частоти, тобто ті, що обчислюються відповідно до певного закону розподілу.

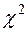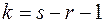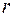Випадкова величина , або критерій Пірсона, розподілена за законом Пірсона з кількістю ступенів свободи , де – кількість параметрів теоретичного закону розподілу, за яким обчислюються теоретичні частоти. Так, для нормального закону 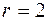, для показникового – 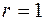, для рівномірного – .

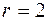Емпіричне значення критерію Пірсона, що обчислюється за формулою (13.7), порівнюють з критичними значеннями 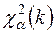. Якщо 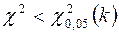, то нульову гіпотезу : 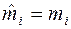нема підстав відхилити, тобто закон розподілу, що припускається, відповідає емпіричним даним, при цьому ми помиляємось в п’яти випадках із ста, приймаючи можливо хибну гіпотезу (похибка другого роду).

Якщо 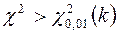, то нульову гіпотезу слід відкинути, тобто розбіжність між емпіричними частотами і частотами, які обчислювались відповідно до певного припущення відносно закону розподілу у генеральній сукупності, є статистично значущою. Отже, приймається альтернативна гіпотеза 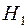: 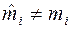. При цьому ми помиляємось в одному випадку із ста, відкидаючи можливо правильну гіпотезу (похибка першого роду).

Якщо , то це область невизначеності, і необхідні додаткові дослідження.

13.6.2. Критерій згоди Колмогорова. Обчислимо теоретичні 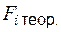та емпіричні 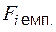значення інтегральної функції розподілу.

Побудуємо випадкову величину:

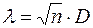, (13.8)

де 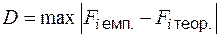, 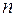– загальна кількість дослідів.

Якщо 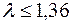, то з надійністю 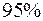гіпотеза 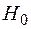: 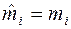приймається; якщо 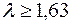то з рівнем значущості 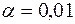гіпотеза 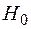відхиляється; якщо 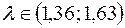– це область невизначеності.

13.6.3. Критерій Романовського. Цей критерій, що використовується для оцінки наближення емпіричного розподілу до теоретичного, базується на визначенні випадкової величини 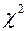за формулою (13.7), яка обчислена у припущенні наявності нормального закону розподілу.

Далі, враховуючи кількість ступенів свободи k, розглядають вираз 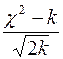. Якщо його величина менше 3, то це дає підстави прийняття теоретичний розподілу за закон розподілу генеральної сукупності.

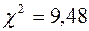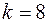Приклад. За результатами дослідження вибіркової сукупності маємо, що та . Перевірити, чи відповідає закон розподілу генеральної сукупності нормального закону розподілу.

Розв’язання. Обчислимо критерій Романовського:

,

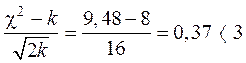Отже, це означає, що закон розподілу у генеральній сукупності можна вважати нормальним.

13.6.4. Критерій Ястремського. Недоліком більшості критеріїв згоди є те, що вони не дають прямої відповіді на питання щодо можливості застосування до даного емпіричного розподілу певного теоретичного розподілу, а вказують лише на ймовірність розбіжності між ними. Цей недолік усувається при використанні критерію Ястремського, який дає пряму відповідь на питання про міру розбіжності між емпіричним та теоретичним розподілом. При побудові критерію Ястремського використовується критерій Пірсона. У загальному вигляді критерій Ястремського можна записати наступним чином:

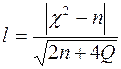, (13.9)

де 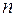– кількість груп;

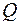– величина, що залежить від кількості груп, але при кількості груп менше 20, приймається рівною 0,6.

Оскільки випадкова величина розподілена за нормальним законом, то з імовірністю 0,997 вона за абсолютною величиною не повинна перевищувати трійку. Таким чином, якщо 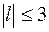, то емпіричний розподіл підпорядковується теоретичному закону розподілу. При 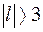емпіричний розподіл не відповідає теоретичному розподілу.

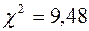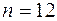Приклад. За результатами дослідження вибіркової сукупності маємо, що , та 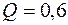. Перевірити, чи відповідає закон розподілу генеральної сукупності нормального закону розподілу.

Розв’язання. Обчислимо критерій Ястремського:

.

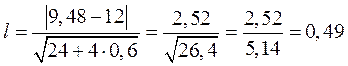Оскільки 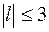, то емпіричний розподіл можна вважати нормальним.

Дата добавления: 2014-01-04