Следствия. 1. Так как -1£ (х, у) /|x||y|£ 1, то мы можем определить угол g между векторами х и у по формуле: g = arccos

1. Так как -1£ (х, у) /|x||y|£ 1, то мы можем определить угол g между векторами х и у по формуле: g = arccos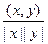. И тогда (х, у) = |x||y|cosg.

2. (х₁у₁ +…+ х_пу_п)² £ (х₁²+…+ х_п²)(у₁²+…+ у_п²) - неравенство Коши-Буняковского для Е = R ⁿ.

3. (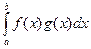)² £ .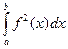

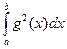4. Неравенство треугольника: | x + y| £ |x| + |y|.

Доказательство. | x + y|² =(х+у, х+у) =(х,х)+(у,у)+2(х,у) £ £ |x|² + |y|² + 2|x|×|y| = (|x| + |y|)².

ÿ

Теорема 4. Если ненулевые векторы а₁,…,а_k Î E такие, что а_i ^ а_j при i ¹ j, то а₁,…,а_k – линейно независимы.

Доказательство. Пусть a₁а₁ +…+a_kа_k = 0. Тогда

(a₁а₁ +…+a_kа_k, а_i)= a_i (а_i, а_i)= 0 Þ a_i = 0 " = i.

ÿ

Пусть е Î Е, < е > = L, L ^{^} = { xÎ E| (x, е) = 0 }.

Теорема 5. L ^{^} - подпространство в Е, и Е = L Å L ^{^}.

Доказательство. Очевидно, если х, у Î L ^{^}, то (x, е) = 0,

(у, е) = 0 Þ (x + у, е) = (x, е) + (у, е)= 0 + 0 = 0, и для a Î Р

(ax, е) = a(x, е) = a×0 = 0 Þ х + у, ax Î L ^{^}. И кроме того, очевидно, 0Î L ^{^}. Следовательно, L ^{^} - подпространство.

По теореме 2 " хÎ Е х = a е + z, a е Î L, zÎ L ^{^} Þ

Е = L + L ^{^}. Так же если LL ^{^} ' g е, то (g е, е) = 0 Þ g = 0 Þ

LL ^{^} = {0} Þ Е = L Å L ^{^}.

ÿ

Теорема 6. Пусть dimE = n. Тогда в Е существует ортогональный базис {e₁,…,e_n }, то есть такой базис, что (e_i,e_j)= 0 при i ¹ j.

Доказательство индукцией по п. При п = 1 доказывать нечего. Пусть утверждение верно для п – 1. Выберем еÎ Е, е ¹ 0. Положим е₁= е, L = <е₁>. Тогда, очевидно, L ^{^} является евклидовым пространством, и dim L ^{^} = n –1. По предположению индукции можно считать, что в L ^{^} ортогональный базис {e₂,…,e_n} существует. Тогда {e₁,e₂,…,e_n} по теореме 5 - ортогональный базис в Е.

ÿ

Теорема 7. Пусть dimE = n. Тогда в Е существует ортонормированый базис {и₁,…,и_n}, то есть такой базис, что

(и_i, и_j)= d_ij =

Доказательство. Рассмотрим ортогональный базис

{e₁,…,e_n}. Тогда векторы и_i = e_i/|e_i|, i =1,…,n, образуют ортонормированный базис.

ÿ

Очевидно, для ортогонального базиса матрица Грама диагональна, а для ортонормированного базиса Г = Е.

Определение. Отображение j: Е₁® Е₂ евклидовых пространств называется изоморфизмом евклидовых пространств, если j - изоморфизм линейных пространств, сохраняющий скалярное произведение, то есть (j х,j у) = (х, у) " х, у Î Е₁. В этом случае евклидовы пространства Е₁ и Е₂ называются изоморфными, что обозначается так: Е₁» Е₂.

Теорема 8. Если Е – евклидово пространство и dim E= п, то Е» Rⁿ.

Доказательство. Пусть {и₁,…,и_n} – ортонормированный

базис в Е, 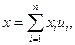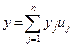. Тогда (х,у)= х₁у₁+…+ х_п у_п.

Отсюда следует, что отображение j: Е ® Rⁿ такое, что

jх=(х₁,…,х_п), является изоморфизмом евклидовых пространств, так как из п. 7.3 это изоморфизм линейных пространств, и (j х,j у) = (х, у) = х₁у₁+…+ х_п у_п.

ÿ

Следствие. Из теоремы 8 следует, что все евклидовы пространства одной размерности изоморфны. И значит, пространства изоморфны тогда и только тогда, когда у них одинаковая размерность. Таким образом, класс изоморфных друг другу евклидовых пространств полностью задается размерностью любого из этих пространств. И для любой размерности п с точностью до изоморфизма существует лишь одно пространство размерности п. Например, пространство

R ⁿ. Все остальные пространства размерности п ему изоморфны.

Далее n- мерное евклидово пространство мы будем обозначать Е^п.

Лекция 30.

Пусть EÊL – подпространство, L ^{^} ={xÎЕ |(x, y)=0 "yÎL}= = {xÎЕ | x ^ L}.

Упражнение. Доказать, что L ^{^} - подпространство.

Определение. Подпространство L ^{^} называется ортогональным дополнением к подпространству L.

Теорема 9. Е^п = L Å L ^{^}.

Доказательство. Если х Î L 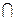L ^{^}, то х ^ х Þ (х, х)= 0 Þ

х = 0 Þ L 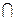L ^{^} = 0 Þ L + L ^{^} = L Å L ^{^}.

Докажем, что L + L ^{^} = Е^п. Пусть х Î Е^п. Покажем, что

можно представить х в виде х = а + b, где а Î L, bÎ L ^{^}. Выберем в L ортонормированный базис {и₁,…,и_k}. Будем искать а в виде а = a₁и₁+…+a_kи_k, где a₁,…,a_k такие, что

b = (х – а) ^ L, то есть " i (x – a, и_i)= 0 Û (a, и_i)= (x, и_i) Û

(a₁и₁+…+a_kи_k, и_i)= (x, и_i) Û (a_iи_i, и_i)= (x, и_i) Û a_i = (x, и_i).

Таким образом, мы показали, что a_i $!, то есть а находится однозначно, и значит, однозначно определяется и b. Отсюда следует не только равенство Е^п=L+L ^{^}, но и ещё раз мы получили, что Е^п = L Å L ^{^}.

ÿ

Теорема 10. L₁ ^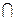{^} L₂ ^{^} = (L₁ + L₂) ^{^}.

Доказательство. Если хÎ L₁ ^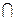{^} L₂ ^{^}, то (х, а) = 0 "аÎ L₁, (х, b) = 0 "bÎL₂ Þ (х, a+b)= 0 Þ x ^ (L₁+ L₂), хÎ(L₁+ L₂) ^{^}.

Если же хÎ(L₁+ L₂) ^{^}, то (х, а+b) = 0 "аÎL₁, "bÎL₂ Þ при b = 0 (х, а) = 0 "аÎL₁ Þ хÎ L₁ ^{^}. Аналогично, при а = 0 получаем, что хÎ L₂ ^{^}. И следовательно, хÎ L₁ ^{^} L₂ ^{^}.

ÿ

Определение. Говорят, что подпространство L₂ ортогонально подпространству L₁, L₂ ^ L₁, если "bÎ L₂, "аÎ L₁, (а, b) = 0.

Дата добавления: 2014-01-04