Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи

Обернена теорема: Якщо сума квадратів двох сторін трикутника дорівнює квадрату третьої сторони, те цей трикутник прямокутний.

За допомогою теореми Піфагора доводяться наведені далі твер­дження.

1. У рівнобедреному прямокутному трикутнику гострі кути дорівнюють по 45°, а відношення гіпотенузи до катета дорівнює

Для прямокутного трикутника (див. рис. 1):

· синус гострого кута дорівнює відношенню катета, протилежного цьому куту, до гіпотенузи;

· косинус гострого кута дорівнює відношенню катета, прилеглого до цього кута, до гіпотенузи;

· тангенс гострого кута дорівнює відношенню катета, протилежного цьому куту, до катета, прилеглого до нього.

Таким чином, згідно з рис. 1 маємо:

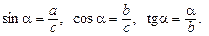
Теорема косинусів. Квадрат сторони трикутника дорівнює сумі квадратів двох інших його сторін мінус подвоєний добуток цих сторін на косинус кута між ними (рис. 2):

с ² = а ² + b ² – 2 ab cos γ.

Теорема синусів. Відношення сторони трикутника до синуса протилежного кута є величина стала для даного трикутника, що дорівнює двом радіусам описаного кола (рис. 2):

Рис. 2

Задача. У трикутнику дано три сторони а, b, с. Знайти довжину медіани, проведеної до сторони а.

Ø Нехай ADC = φ, AD = m_a — медіана Δ АВС (рис. 3). Маємо ADB = 180° — φ. Запишемо теорему косинусів для трикутників ADC і ADB:

Рис. 3

Додавши ці рівняння почленно і врахувавши рівність cos (180° –
– φ) = –cos φ, дістанемо:

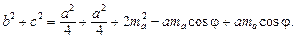
Після елементарних перетворень знайдемо

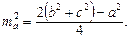
Дата добавления: 2014-01-04