
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Пусть е – произвольный базис в линейном пространстве L над R
|
|
|
|
Критерий Сильвестра.
Пусть е – произвольный базис в линейном пространстве L над R. Для квадратичной формы F обозначим через Мk левый угловой минор порядка k матрицы [ F ] в базисе е: Мk =  .
.
Теорема (критерий Сильвестра положительной определенности квадратичной формы). F > 0 Û все Мk > 0.
Þ. Пусть F > 0. Тогда в некотором базисе е¢ форма F имеет
нормальный вид, и  = Е. Если Т =
= Е. Если Т =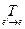 , то
, то 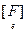 = Т t
= Т t  T = =Т tЕТ= Т tТ, и det [ F ] = |Т tТ| = |T|2 > 0. Рассмотрим подпространство Lk= <е1,е2,…,еk>. Очевидно, ограничение формы F на это подпространство
T = =Т tЕТ= Т tТ, и det [ F ] = |Т tТ| = |T|2 > 0. Рассмотрим подпространство Lk= <е1,е2,…,еk>. Очевидно, ограничение формы F на это подпространство 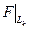 > 0 Þ det
> 0 Þ det  = Мk > 0 " k.
= Мk > 0 " k.
Ü. Пусть все Мk > 0. Тогда det [ F ] = Мп > 0. Рассмотрим подпространство Lп-1 = <е1,…,еп-1>. Заменим базисный вектор еп на базисный вектор ип, f- ортогональный к Lп-1. Для этого будем искать ип в виде ип = еп - a1е1 -…- aп-1еп-1, причём потребуем, чтобы при i =1,…, п-1 f(ип , еi)= 0. Запишем эти уравнения в виде f(еп - a1е1 -…- aп-1еп-1, еi)= 0 или в виде f(a1е1 +…+ aп-1еп-1, еi) = f(eп , еi). Воспользовавшись линейностью f по первому аргументу, получим систему
(п-1)-го линейного уравнения с (п-1) неизвестным a1,…,aп-1: a1f(е1,еi)+…+aп-1f(еп-1, еi)= f(eп , еi), i =1,…, п-1. Определителем этой системы является Мп-1 ¹ 0. Поэтому у этой системы существует единственное решение, которое можно найти, например, по правилу Крамера. Очевидно, система векторов е¢ = {е1,…,еп-1,uп} линейно независима, то есть является базисом в L. В этом базисе
 , и det
, и det 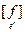 = Мп-1 × lп > 0. Так
= Мп-1 × lп > 0. Так
как Мп-1>0, то lп> 0. Далее мы от еп-1 перейдем к ип-1, f- ор- тогональному к Lп-2, и получим lп-1> 0, и т.д. В конце концов мы получим базис и, в котором 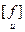 = diag(l1,…, ln),
= diag(l1,…, ln),
F(y) = l1y12+…+lnyn2. Так как все li > 0, то F > 0.
ÿ
Лекция 36.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 380; Нарушение авторских прав?; Мы поможем в написании вашей работы!