Замечания

1. Функции, для которых выполнены условия 1, 2 из определения и 1, 2 из следствия называются полуторалинейными (они линейны по первому аргументу и полулинейны по второму). Таким образом, любая эрмитова функция - полуторалинейная.

2. Теория эрмитовых функций аналогична теории симметричных билинейных функций, поэтому многие утверждения будут лишь сформулированы, а их доказательства читателю предлагается провести в качестве упражнений.

Примером эрмитовой функции служит скалярное произведение на унитарном пространстве.

Пусть f - полуторалинейная функция на n -мерном пространстве L = Lⁿ над полем С, e = {e₁, …,e_n} – произвольный

базис в L. Если x, yÎ L, где все

x_s, y_tÎ С, то f(x,y) = . Из

этой формулы видно, что значение полуторалинейной функции f(x, y) при произвольных x, yÎ L полностью и однозначно определяется n² значениями f_st = f(e_s,e_t) функции f на упорядоченных парах базисных векторов e_s, e_t.

Матрицу [ ] =(f_st)_s,t=1,…,n будем называть матрицей полуторалинейной функции f в базисе e.

Пусть . Тогда f(x,y)=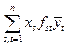= 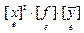, то есть функция f(x, y) является многочленом, все одночлены которого – первой степени от координат вектора х и первой степени от координат вектора . Такой многочлен является линейной формой по х и полулинейной по у, то есть полуторалинейной формой. Полуторалинейные формы, соответствующие эрмитовым функциям, будем называть эрмитовыми формами. Необходимым и достаточным условием эрмитовости полуторалинейной формы f явлется условие f_ts = f(e_t,e_s)= = " s,t, то есть [ ] ^t= в любом (в некотором) базисе е – это условие эрмитовости её матрицы [ ] в любом (в некотором) базисе е.

Определение. Пусть f - полуторалинейная функция на линейном пространстве L над С. Функция F: L ® С, заданная формулой F(x) = f(x, x) " x Î L, называется квадратичной функцией, определяемой полуторалинейной функцией f. Если f – эрмитова, то и F называется эрмитовой.

Очевидно, если f(x, y) =, то F(x) = -

форма второй степени от действительных и мнимых частей

координат х.

Матрицей квадратичной формы F будем называть матрицу соответствующей полуторалинейной формы f: [ ] = [ ]. И тогда F(x) = .

Упражнение. Проверить, что полуторалинейная форма f однозначно восстанавливается из определенной ею квадратичной формы F по формуле

f(x, y)=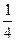(F(x+y) - F(x - y) + iF(x+iy) - iF(x - iy)). (26.1)

Если e ¢ = {e¢₁,…,e¢_n} - другой базис в L, и Т = 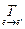= (t_ks) - матрица перехода от базиса e к базису e ¢, то

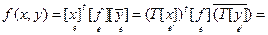
. Сле-

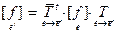довательно, , или , где 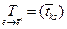- матрица перехода от базиса e к «комплексно сопряженному» с e¢ базису 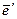, состоящему из векторов

, s=1,…,n. Аналогично, .

Дата добавления: 2014-01-04